SmartyPants
- 15
- 1
- TL;DR
- integrating w/ respect to y yields the correct answer, but I can't get to the same result when integrating w/ respect to x
**EDIT** Everything looked good in the preview, then I posted and saw that some stuff got cropped out along the right edge...give me some time and I'll fix it.
Hello all,
I"m trying to calculate shaded area, that is, the area bounded by the curves ##x=y^{2}-2, x=e^{y}, y=-1##, and ##y=1##:
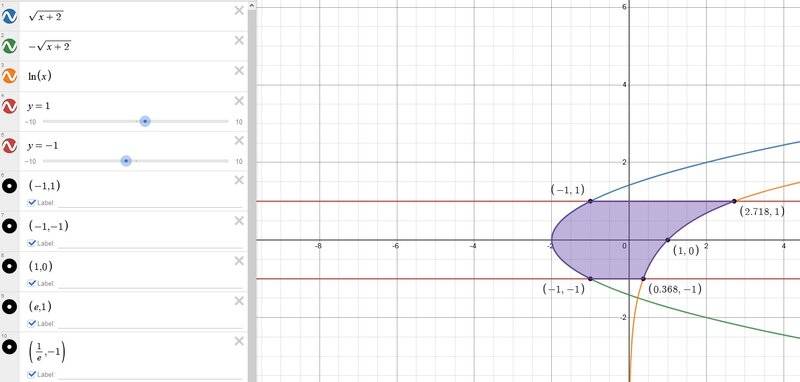
Integrating w/ respect to ##y## is easy simply because 1) the curves are initially presented to us as functions of ##y##, not ##x##, and 2) we can see that it can be calculated with a single integral:
$$\int\limits_{\scriptsize -1}^{\scriptsize 1}({e^{y}-(y^2-2)}){\;\mathrm{d}y}=\int\limits_{\scriptsize -1}^{\scriptsize 1}({e^{y}-y^2+2}){\;\mathrm{d}y}=\left[e^y-\frac{y^3}{3}+2y\right]{1\atop-1}=\left[e^{(1)}-\frac{(1)^{3}}{3}+2(1)\right]-\left[e^{(-1)}-\frac{(-1)^{3}}{3}+2(-1)\right]$$ $$=\left[e-\frac{1}{3}+2\right]-\left[\frac{1}{e}+\frac{1}{3}-2\right]=e-\frac{1}{3}+2-\frac{1}{e}-\frac{1}{3}+2=\frac{12}{3}-\frac{2}{3}-\frac{1}{e}+e=\frac{10}{3}-\frac{1}{e}+e\approx 5.684$$
...this is the correct answer (as far as I know)...
But of course I couldn't leave well enough alone and decided to do it the hard way (that is, calculate the area by integrating w/ respect to ##x##) as well just for self-edification. Unfortunately I'm not getting the same answer and it's driving me nuts . It must be a simple arithmetic or sign error or something, because I'm pretty sure my integration and bounds are correct. Here's how I went about it. First I split up the area into sub-areas according to all the different bounds of integration:
. It must be a simple arithmetic or sign error or something, because I'm pretty sure my integration and bounds are correct. Here's how I went about it. First I split up the area into sub-areas according to all the different bounds of integration:
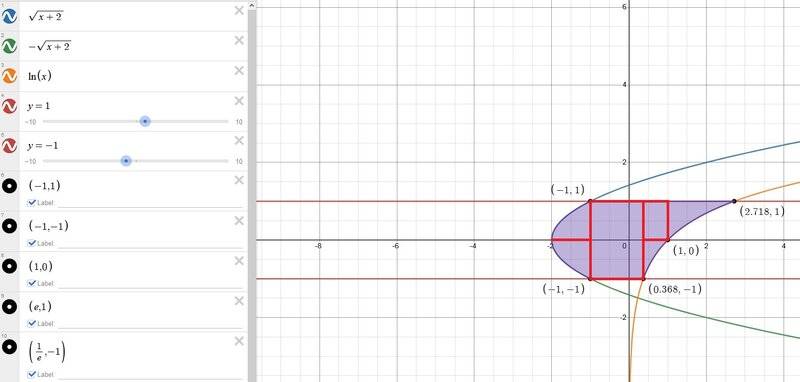
1. First shaded area from ##x=-2## to ##x=-1##:
We see that the vertex of the parabola ##x=y^2-2## is at the point ##(-2,0)##, and that it intercepts the lines ##y=-1## and ##y=1## at the points ##(-1,1)## and ##(-1,-1)##.
Now ##x=y^2-2## is just ##y=\pm \sqrt{x+2}##, so we can just integrate ##y=\sqrt{x+2}## from ##-2## to ##-1## and multiply by two to get the shaded area from ##x=-2## to ##x=-1##:
$$2\int\limits_{\scriptsize -2}^{\scriptsize -1}{\sqrt{x+2}}{\;\mathrm{d}x}=2\int\limits_{\scriptsize -2}^{\scriptsize -1}{\left(x+2\right)^{\frac{1}{2}}}{\;\mathrm{d}x}=2\left[\frac{2}{3}\,\left(x+2\right)^{\frac{3}{2}}\right]{-1\atop-2}=\frac{4}{3}\,\left[\left(\sqrt{x+2}\right)^{3}\right]{-1\atop-2}=\frac{4}{3}\,\left[\left(\sqrt{(-1)+2}\right)^{3}-\left(\sqrt{(-2)+2}\right)^{3}\right]$$ $$=\frac{4}{3}\,\left[1-0\right]=\frac{4}{3}$$
2. The 2nd shaded area is just a rectangle, so no caclulus needed this time (it's just width times height)...but we need to know where ##x=e^y## (which is just ##y=ln(x)##) intercepts ##y=-1##. Some quick math shows us that this point on intersection is ##(1/e, -1)##. Thus the area of this rectangle is its width ##\left| -1-\frac{1}{e}\right|## times its height ##2##, which is just ##\left(1+\frac{1}{e}\right)\cdot 2=2+\frac{2}{e}##.
3. The 3rd shaded area is between the curve ##y=ln(x)## and ##x##-axis from ##x=1/e## to ##x=1## (since that's where the function ##y=ln(x)## intercepts the ##x##-axis):
##\int\limits_{\scriptsize \frac{1}{e}}^{\scriptsize 1}{\ln\left(x\right)}{\;\mathrm{d}x}\rightarrow## let ##u=ln(x)\rightarrow du=\frac{1}{x}dx##; also let ##dx=dv\rightarrow v=x\rightarrow## ##\int\limits_{\scriptsize \frac{1}{e}}^{\scriptsize 1}{u}{\;\mathrm{d}v}=u\,v-\int\limits_{\scriptsize \frac{1}{e}}^{\scriptsize 1}{v}{\;\mathrm{d}u}=x\,\ln\left(x\right)-\int\limits_{\scriptsize \frac{1}{e}}^{\scriptsize 1}{x\cdot \frac{1}{x}}{\;\mathrm{d}x}=x\,\ln\left(x\right)-\int\limits_{\scriptsize \frac{1}{e}}^{\scriptsize 1}{1}{\;\mathrm{d}x}=\left[x\,\ln\left(x\right)-x\right]{1\atop1/e}## ##=(1\,\ln\left(1\right)-1)-(1/e\,\ln\left(1/e\right)-1/e)## ##=(1(0)-1)-(\frac{1}{e}\cdot \left(-1\right)-\frac{1}{e})=(-1)-\left(-\frac{2}{e}\right)=\frac{2}{e}-1\rightarrow## Since this value is negative, we'll take its aboslute value ##\rightarrow## This gives us an area of ##\left | \frac{2}{e}-1 \right |=1-\frac{2}{e}##
4. The 4th shaded area is the small rectangle directly above the area we just calculated inthe previous step. Its area is width times height, which is just ##\left(1-\frac{1}{e}\right)\cdot 1=1-\frac{1}{e}##
5. And finally the 5th shaded area is the area between the curve ##y=ln(x)## and ##y=1##. We see that the lower bound of integration is ##x=1##, and with some quick math, we see that the upper bound is ##x=e##, since that's where the curve ##y=ln(x)## intercepts the line ##y=1##:
$$\int\limits_{\scriptsize 1}^{\scriptsize e}{1-\ln\left(x\right)}{\;\mathrm{d}x}=\int\limits_{\scriptsize 1}^{\scriptsize e}{1}{\;\mathrm{d}x}-\int\limits_{\scriptsize 1}^{\scriptsize e}{\ln\left(x\right)}{\;\mathrm{d}x}=\left[x-(x\,\ln\left(x\right)-x)\right]{e\atop1}=\left[x\,\ln\left(x\right)\right]{e\atop1}=e\,\ln\left(e\right)-1\,\ln\left(1\right)=1-0=1$$
Finally I can sum my calculated areas to get the total area:
$$\frac{4}{3}+2+\frac{2}{e}+1-\frac{2}{e}+1-\frac{1}{e}+1=\frac{19}{3}-\frac{1}{e}\approx 5.965$$
...this is close to [but not equal to] the answer I got when integrating w/ respect to ##y##. I've been over it several times and just can't figure it out. I must be making a small mistake somewhere. Any help would be appreciated.
Eric
Hello all,
I"m trying to calculate shaded area, that is, the area bounded by the curves ##x=y^{2}-2, x=e^{y}, y=-1##, and ##y=1##:
Integrating w/ respect to ##y## is easy simply because 1) the curves are initially presented to us as functions of ##y##, not ##x##, and 2) we can see that it can be calculated with a single integral:
$$\int\limits_{\scriptsize -1}^{\scriptsize 1}({e^{y}-(y^2-2)}){\;\mathrm{d}y}=\int\limits_{\scriptsize -1}^{\scriptsize 1}({e^{y}-y^2+2}){\;\mathrm{d}y}=\left[e^y-\frac{y^3}{3}+2y\right]{1\atop-1}=\left[e^{(1)}-\frac{(1)^{3}}{3}+2(1)\right]-\left[e^{(-1)}-\frac{(-1)^{3}}{3}+2(-1)\right]$$ $$=\left[e-\frac{1}{3}+2\right]-\left[\frac{1}{e}+\frac{1}{3}-2\right]=e-\frac{1}{3}+2-\frac{1}{e}-\frac{1}{3}+2=\frac{12}{3}-\frac{2}{3}-\frac{1}{e}+e=\frac{10}{3}-\frac{1}{e}+e\approx 5.684$$
...this is the correct answer (as far as I know)...
But of course I couldn't leave well enough alone and decided to do it the hard way (that is, calculate the area by integrating w/ respect to ##x##) as well just for self-edification. Unfortunately I'm not getting the same answer and it's driving me nuts
 . It must be a simple arithmetic or sign error or something, because I'm pretty sure my integration and bounds are correct. Here's how I went about it. First I split up the area into sub-areas according to all the different bounds of integration:
. It must be a simple arithmetic or sign error or something, because I'm pretty sure my integration and bounds are correct. Here's how I went about it. First I split up the area into sub-areas according to all the different bounds of integration:1. First shaded area from ##x=-2## to ##x=-1##:
We see that the vertex of the parabola ##x=y^2-2## is at the point ##(-2,0)##, and that it intercepts the lines ##y=-1## and ##y=1## at the points ##(-1,1)## and ##(-1,-1)##.
Now ##x=y^2-2## is just ##y=\pm \sqrt{x+2}##, so we can just integrate ##y=\sqrt{x+2}## from ##-2## to ##-1## and multiply by two to get the shaded area from ##x=-2## to ##x=-1##:
$$2\int\limits_{\scriptsize -2}^{\scriptsize -1}{\sqrt{x+2}}{\;\mathrm{d}x}=2\int\limits_{\scriptsize -2}^{\scriptsize -1}{\left(x+2\right)^{\frac{1}{2}}}{\;\mathrm{d}x}=2\left[\frac{2}{3}\,\left(x+2\right)^{\frac{3}{2}}\right]{-1\atop-2}=\frac{4}{3}\,\left[\left(\sqrt{x+2}\right)^{3}\right]{-1\atop-2}=\frac{4}{3}\,\left[\left(\sqrt{(-1)+2}\right)^{3}-\left(\sqrt{(-2)+2}\right)^{3}\right]$$ $$=\frac{4}{3}\,\left[1-0\right]=\frac{4}{3}$$
2. The 2nd shaded area is just a rectangle, so no caclulus needed this time (it's just width times height)...but we need to know where ##x=e^y## (which is just ##y=ln(x)##) intercepts ##y=-1##. Some quick math shows us that this point on intersection is ##(1/e, -1)##. Thus the area of this rectangle is its width ##\left| -1-\frac{1}{e}\right|## times its height ##2##, which is just ##\left(1+\frac{1}{e}\right)\cdot 2=2+\frac{2}{e}##.
3. The 3rd shaded area is between the curve ##y=ln(x)## and ##x##-axis from ##x=1/e## to ##x=1## (since that's where the function ##y=ln(x)## intercepts the ##x##-axis):
##\int\limits_{\scriptsize \frac{1}{e}}^{\scriptsize 1}{\ln\left(x\right)}{\;\mathrm{d}x}\rightarrow## let ##u=ln(x)\rightarrow du=\frac{1}{x}dx##; also let ##dx=dv\rightarrow v=x\rightarrow## ##\int\limits_{\scriptsize \frac{1}{e}}^{\scriptsize 1}{u}{\;\mathrm{d}v}=u\,v-\int\limits_{\scriptsize \frac{1}{e}}^{\scriptsize 1}{v}{\;\mathrm{d}u}=x\,\ln\left(x\right)-\int\limits_{\scriptsize \frac{1}{e}}^{\scriptsize 1}{x\cdot \frac{1}{x}}{\;\mathrm{d}x}=x\,\ln\left(x\right)-\int\limits_{\scriptsize \frac{1}{e}}^{\scriptsize 1}{1}{\;\mathrm{d}x}=\left[x\,\ln\left(x\right)-x\right]{1\atop1/e}## ##=(1\,\ln\left(1\right)-1)-(1/e\,\ln\left(1/e\right)-1/e)## ##=(1(0)-1)-(\frac{1}{e}\cdot \left(-1\right)-\frac{1}{e})=(-1)-\left(-\frac{2}{e}\right)=\frac{2}{e}-1\rightarrow## Since this value is negative, we'll take its aboslute value ##\rightarrow## This gives us an area of ##\left | \frac{2}{e}-1 \right |=1-\frac{2}{e}##
4. The 4th shaded area is the small rectangle directly above the area we just calculated inthe previous step. Its area is width times height, which is just ##\left(1-\frac{1}{e}\right)\cdot 1=1-\frac{1}{e}##
5. And finally the 5th shaded area is the area between the curve ##y=ln(x)## and ##y=1##. We see that the lower bound of integration is ##x=1##, and with some quick math, we see that the upper bound is ##x=e##, since that's where the curve ##y=ln(x)## intercepts the line ##y=1##:
$$\int\limits_{\scriptsize 1}^{\scriptsize e}{1-\ln\left(x\right)}{\;\mathrm{d}x}=\int\limits_{\scriptsize 1}^{\scriptsize e}{1}{\;\mathrm{d}x}-\int\limits_{\scriptsize 1}^{\scriptsize e}{\ln\left(x\right)}{\;\mathrm{d}x}=\left[x-(x\,\ln\left(x\right)-x)\right]{e\atop1}=\left[x\,\ln\left(x\right)\right]{e\atop1}=e\,\ln\left(e\right)-1\,\ln\left(1\right)=1-0=1$$
Finally I can sum my calculated areas to get the total area:
$$\frac{4}{3}+2+\frac{2}{e}+1-\frac{2}{e}+1-\frac{1}{e}+1=\frac{19}{3}-\frac{1}{e}\approx 5.965$$
...this is close to [but not equal to] the answer I got when integrating w/ respect to ##y##. I've been over it several times and just can't figure it out. I must be making a small mistake somewhere. Any help would be appreciated.
Eric
 .
.