cppIStough
- 24
- 2
I have a spherical cap of liquid (drop) that rests on a substrate. The substrate has a small hole at the base where liquid is pumped into the drop. One way to parameterize the spherical cap is via: $$x = \sin(s)\cos\phi/\sin\alpha, \,\,\,y= \sin(s)\sin\phi/\sin\alpha,\,\,\,z=(\cos(s)-\cos\alpha)/\sin\alpha$$ where here ##\alpha## is the angle the spherical cap makes with the x-y plane, and ##\phi \in [0,2\pi]## and ##s\in[0,\alpha]##.
Now ##\eta## is a small disturbance to the drop. The author then states the volume change can be written as $$\Delta V = \int_0^{2\pi}\int_{\cos\alpha}^1 R^2 \eta d(\cos(s))d\phi$$
Can someone explain the math behind that integral? I understand the ##\phi## integral, but the inside integral I can't make sense of. For help, here's a sketch:
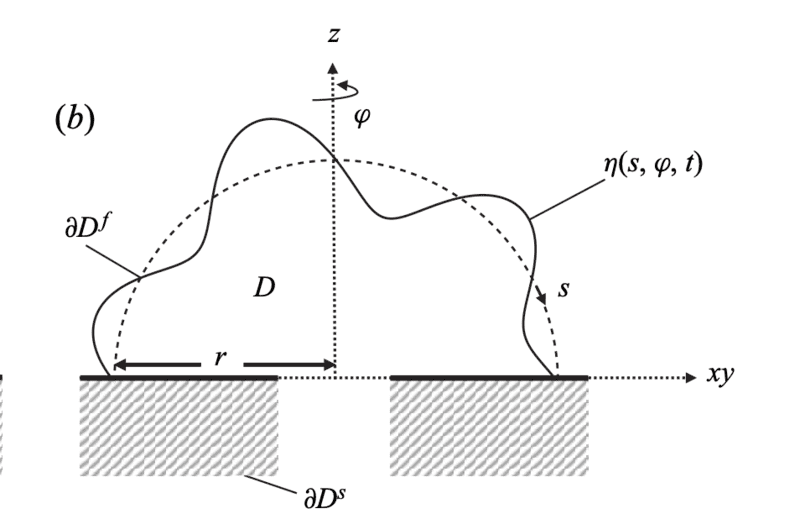
Now ##\eta## is a small disturbance to the drop. The author then states the volume change can be written as $$\Delta V = \int_0^{2\pi}\int_{\cos\alpha}^1 R^2 \eta d(\cos(s))d\phi$$
Can someone explain the math behind that integral? I understand the ##\phi## integral, but the inside integral I can't make sense of. For help, here's a sketch:
Last edited by a moderator: