Integrating a Function over a Torus Contour

[aheight]

I'd like to integrate a function over a closed circle-like contour around an arbitrary point on a torus and I assume I would use the expression:

$$ \int_{t_1}^{t_2} f(x,y,z) \sqrt{x'(t)^2+y'(t)^2+z'(t)^2}dt$$

And I cannot come up with an explicit parameterization of the variables in terms of t. Here's what I have:

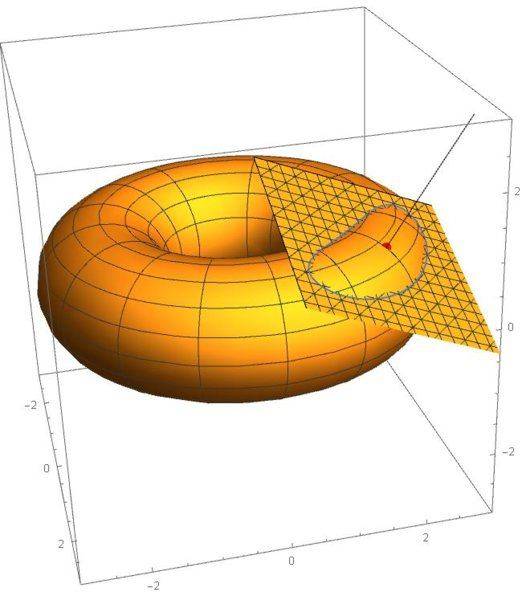
The torus is given by $\{(R+\rho \cos(\alpha))\cos(\phi),(R+\rho \cos(\alpha))\sin(\phi), \rho \sin(\phi)\}$ or $(x^2+y^2+z^2+b^2-a^2)^2=4b^2(x^2+y^2)$. Let's just use R=2 and $\rho=1$ and let me pick a point on the torus with $\alpha=\pi/3$ and $\rho=\pi/4$. I now want to draw a small closed circle-like contour around that point on the torus so I'll just use a torus section consisting of a plane slicing through the torus and normal to the surface at the point and a little below it. That plane is given by: $$ n_x(x-a x_1)+n_y(y-a y_1)n_z(z-a z_1)=0$$ with $a$ being a scale factor say $a=0.9$. The plot below is what that looks like. So where the plane intersects the torus is my blue contour. So that I need $$\int_{\text{blue}} f(x,y,z) \sqrt{x'(t)^2+y'(t)^2+z'(t)^2}dt$$

I can solve for the solution set numerically and then do some curve-fitting for $x(t),y(t),z(t)$.

So I was wondering if there is a more elegant way to paramaterize x, y and z in this case or how to do the integration in general?
Thanks for reading.

 

[andrewkirk]

Does the curve have to be circle-like? If not, an easier contour would be a 'rectangle' that follows the iso lines of $\alpha$ and $\phi$, assuming those are the two coordinates for the surface in an angular coordinate system.

Given your point is $\alpha=\pi/3,\ \phi=\pi/4$, you could make the curve go around the rectangle with segments:

• $\alpha=\pi/6,\ \phi\in[\pi/8,3\pi/8]$
• $\alpha\in [\pi/6,3\pi,6],\ \phi=3\pi/8$
  
• $\alpha=3\pi/6,\ \phi\in[\pi/8,3\pi/8]$
• $\alpha\in [\pi/6,3\pi,6],\ \phi=\pi/8$

Then the integral is simply the sum of four quasi-linear integrals.

 

[aheight]

Thanks! Then I want to show:

$$\int_{\text{blue}} f(x,y,z) \sqrt{x'(t)^2+y'(t)^2+z'(t)^2}dt=\int_{\text{red}} f(x,y,z) \sqrt{x'(t)^2+y'(t)^2+z'(t)^2}dt=0$$

in the plot below where the colors and grid lines reflect a double-cover of the complex plane mapped conformally onto the torus. Should be zero I think. Never did this kind of integration before.

 

[andrewkirk]

Thanks! Then I want to show:

$$\int_{\text{blue}} f(x,y,z) \sqrt{x'(t)^2+y'(t)^2+z'(t)^2}dt=\int_{\text{red}} f(x,y,z) \sqrt{x'(t)^2+y'(t)^2+z'(t)^2}dt=0$$

in the plot below where the colors and grid lines reflect a double-cover of the complex plane mapped conformally onto the torus. Should be zero I think. Never did this kind of integration before.View attachment 222244

Does the problem statement specify integration specifically around the blue curve, or just around any simple, closed, collapsible curve that encloses the chosen point? For many problems in physics, especially in electromagnetism, it is only the latter that matters. The exact path of the curve does not.

Also, what is the goal? Have you been given a specific function $f$ and asked to come up with a formula for the integral? Or are you trying to prove that the integral is zero for any simple, closed, collapsible curve and any sufficiently nice function $f$?

 

[aheight]

Also, what is the goal? Have you been given a specific function $f$ and asked to come up with a formula for the integral? Or are you trying to prove that the integral is zero for any simple, closed, collapsible curve and any sufficiently nice function $f$?

Hi,
Yes, I am trying to apply Cauchy's Theorem over the torus. So for an analytic function of the points $p$ on the torus, I would expect to get $$\oint f(p)dp=0$$
However my preliminary calculations using the integrals in $t$ above are not zero. I am beginning to think I do not have the differential form correct. For example, in the integrals in $t$ above, if $f(x,y,z)=1$ then the formulas just give the arc lengths of the curve so is not or never zero. Seems I need $dp$ of the points $p$ on the torus. But I thought $dp=\sqrt{x(t)^2+y(t)^2+z(t)^2}dt$. Perhaps though that is not correct. Maybe if I explain a little, you can help me:

I am mapping a double-cover of the complex plane onto the torus using the function $$f(z)=w=\frac{1}{\sqrt{(1-z^2)(k^2-z^2)}}$$ It's the standard example of a (non-trivial) Riemann surface explained in Introduction to Riemann Surfaces by Springer. Then each point (x,y,z) on the torus then corresponds to the point $p=(z,w)$ of this mapping. So then I would suppose since the torus is now an analytic manifold, for any analytic function of the points $p$ on the torus such as for example $f(p)=z$ or even $f(p)=1$, I would assume: $$\oint f(p)dp=0$$ Surely this must be the case if the mapping is conformal as I believe it is. That is would I would like to show numerically.

Or is this not correct?

 

[andrewkirk]

Are you using the formula in the OP for coordinates in terms of $R,\rho,\alpha,\phi$? If so, that would cause errors because the last coordinate should be $\rho\sin\alpha$, not $\rho\sin\phi$.

Also, you say your point has $\alpha=\pi/3,\rho=\pi/4$. The two coordinate values that need to be specified are $\alpha$ and $\phi$, not $\alpha$ and $\rho$.

 

[aheight]

Are you using the formula in the OP for coordinates in terms of $R,\rho,\alpha,\phi$? If so, that would cause errors because the last coordinate should be $\rho\sin\alpha$, not $\rho\sin\phi$.

Also, you say your point has $\alpha=\pi/3,\rho=\pi/4$. The two coordinate values that need to be specified are $\alpha$ and $\phi$, not $\alpha$ and $\rho$.

Ok, those are typo mistakes in this thread. My calculations do use $\rho\sin\alpha$ and $\phi$ and $\alpha$. The mapping I am using does produce a closed square contour in the z-plane for the red contour (below). So surely if I integrated an analytic function over that contour I would get zero. However I was under the impression I could integrate directly over the torus to get the same results.

 

[FactChecker]

Hi,
Yes, I am trying to apply Cauchy's Theorem over the torus. So for an analytic function of the points $p$ on the torus, I would expect to get $$\oint f(p)dp=0$$
However my preliminary calculations using the integrals in $t$ above are not zero. I am beginning to think I do not have the differential form correct. For example, in the integrals in $t$ above, if $f(x,y,z)=1$ then the formulas just give the arc lengths of the curve so is not or never zero.

That is correct. Cauchy's integral formula does not apply when you are using path length. It applies to the complex integrand $\frac {f(z)} {z-a} dz$. Notice that dz is a complex number.

 

[aheight]

That is correct. Cauchy's integral formula does not apply when you are using path length. It applies to the complex integrand $\frac {f(z)} {z-a} dz$. Notice that dz is a complex number.

Ok I see that now. However I believe I can apply Cauchy's Theorem on the torus nevertheless. I'm just not using the right differential. And unfortunately I make matters unnecessarily confusing in the posts above by using the variable z for two different quantities: Rather, I should (more clearly) use $(x,y,z)\in\mathbb{R}$ to specify the actual torus, $\mathbb{T}^2$ in 3D real space given by $\{(R+\rho\cos(\alpha))\cos(\phi),(R+\rho\cos(\alpha))\sin(\phi),\rho\sin(\alpha)\}$. And then use the complex mapping $p=(u,w)\in\mathbb{C}:w(u)=\frac{1}{\sqrt{(1-u^2)(k^2-u^2)}}$ onto the torus for every point $(x,y,z)\in \mathbb{T}^2$.

And then for every point $p=(u,w)$ on the torus I can write $u=g(\alpha,\phi)$. Then if I parameterize $\alpha$ and $\phi$, I think then for any closed contour over the torus, and any analytic function $f(p)$ of the points $p= (u,w)$ such as $f(p)=u$,

$$\oint_C f(p)dp=\oint_C u\biggr[\frac{\partial u}{\partial \phi}\frac{d\phi}{dt}+\frac{\partial u}{\partial \alpha}\frac{d\alpha}{dt}\biggr]dt=0$$

Surely that would work.

 

[andrewkirk]

I can't make out from your notation what the mapping from $\mathbb C$ to the torus is. In post 5 you have given a function $f:\mathbb C\to\mathbb C$ and then in post 9 you have written $p=(u,w)\in \mathbb C$, which I presume implies that $u$ and $w$ are the real and imaginary parts of the complex number $p$. You said $p$ is a mapping (ie function), which seems odd, as it is presented as a complex number. But you don't appear to have presented a function whose domain is $\mathbb C$ and range is the torus. I suspect there is some implicit identification going on, but it is so implicit that I cannot guess what it is supposed to be. It would be better to make the identification explicit, so we can be clear exactly what we are trying to do.

I would expect a mapping from the complex numbers to the torus to be a function that specifies an image point by its coordinates $(\alpha,\phi)$ or $(x,y,z)$, with each coordinate expressed as a function of the complex number $z$ that is the pre-image point.

 

[aheight]

I can't make out from your notation what the mapping from $\mathbb C$ to the torus is

Hi Andrew,

The mapping uses four Schwarz-Christoffel transformations. It's a little tedious but nicely explained here: http://www.jujusdiaries.com/p/introduction-mathjax.html. Once we obtain the four-color region in the $\zeta$ plane, it is then a simple matter to contort the region first into a tube, then bend it into a torus. So thus, for every point $(x,y,z)$ on the torus, there corresponds a pair of (complex-valued) points $(u,w(u))$ although in the link above $(z,w(z))$ is used. So for the red contour line where $\phi$ is constant, I can paramaterize that line in terms of just $\alpha$, that is $\{x(\alpha),y(\alpha),z(\alpha)\}$, that then gives me the point $(x,y,z)$ on the torus corresponding to a particular value of $\alpha$. But the transformations are bijections so that I can find the (unique) value of $(u,w(u))$ corresponding to that value of $\alpha$. Since in this case $\phi$ is constant, I can then calculate the integral of say $g(u,w(u))=u$ over that leg as:
$$\oint u(\alpha)\frac{du}{d\alpha} d\alpha$$ and then do the remaining legs of the contour similiarly. Surely that would be an example of Cauchy's Theorem on a torus. I think.

 

[aheight]

Since in this case $\phi$ is constant, I can then calculate the integral of say $g(u,w(u))=u$ over that leg as:
$$\oint u(\alpha)\frac{du}{d\alpha} d\alpha$$ and then do the remaining legs of the contour similiarly. Surely that would be an example of Cauchy's Theorem on a torus. I think.

Just want to follow up on that today: I checked it numerically and the integral is virtually zero. The plot below shows the color-coded contour over which I'm integrating. For example, in the case of the red contour, I invert the transforms to obtain $z(\phi)$ using elliptic functions and compute:
$$\int_{\text{Red}} f(z)\frac{dz}{d\phi} d\phi$$
and then the others similiarly, with the sum of theses on the order of $10^{-17}$. And encouragingly, is also on that order when $f(z)=\frac{1}{\sqrt{(1-z^2)(k^2-z^2)}}$ since the contour does not enclose any of the singular points.

Here is the Mathematia code I used to compute the integral over the red contour:

{(R + \[Rho]*Cos[\[Alpha]])*Cos[\[Phi]], (R + \[Rho]*Cos[\[Alpha]])*Sin[\[Phi]], \[Rho]*Sin[\[Alpha]]}
theX[\[Alpha]_, \[Phi]_] := (R + \[Rho]*Cos[\[Alpha]])*Cos[\[Phi]];
theY[\[Alpha]_, \[Phi]_] := (R + \[Rho]*Cos[\[Alpha]])*Sin[\[Phi]];
theZ[\[Alpha]_, \[Phi]_] := \[Rho]*Sin[\[Alpha]];
theA = 1.5312624348967;
theK = 1.6983963730242;
myFunction[(z_)?NumericQ] := z;
myAlpha = Pi/3 - 0.4;
eta = NIntegrate[1/(2 + Cos[t]), {t, 0, myAlpha}]
myZ1[phi_] := Sin[JacobiAmplitude[(phi + eta*I)*(theK/theA), 1/theK^2]];
myZ1D[phi_] = D[myZ1[phi], phi];
pp1 = ParametricPlot[{Re[myZ1[p]], Im[myZ1[p]]}, {p, Pi/4 - 0.2, Pi/4 + 0.2}];
n1 = NIntegrate[myFunction[myZ1[\[Phi]]]*myZ1D[\[Phi]] /. \[Alpha] -> Pi/3 - 0.4, {\[Phi], Pi/4 - 0.2, Pi/4 + 0.2}]

 

[andrewkirk]

with the sum of theses on the order of $10^{-17}$

I'd be happy with that. I'm currently trying to map a geodesic on an oblate spheroid and the errors arising in my Runge-Kutta results are of the order of 10^-2 or worse. If I could get them under 10^-6 I think I'd declare the problem solved!

 

[aheight]

Now that I have some sort of handle on integrating over the torus, I wonder what's the value of
$$\oint_C f(p)dp$$
with $f(p)=w(z)=\frac{1}{\sqrt{(1-z^2)(k^2-z^2)}}$ and the contour is an analytically-continuous path wrapping around the singular points 1 and k so basically
$$\oint_C \frac{1}{\sqrt{(1-z^2)(k^2-z^2)}} dz.$$ And of course we don't need to integrate over the torus to compute that, we could do it equally-well over the z-plane, and use that as a check for the work over the torus. But for me, working with the torus exemplifies what I believe is Riemann's most interesting contribution to mathematics: Riemann surfaces. :)

So I have a question: Is that path a figure-8 over the torus, as I think it is over the z-plane, or is it a (non-intersecting) circular contour wrapping around 1 and k in the plot below? I don't know.

 

[andrewkirk]

On your diagram the blue-green path is not a figure eight but looks like a simple closed curve that is path-homotopic to a point. However to collapse it homotopically to a point will require moving it to or over the singularity point which you have labelled as 1 on your diagram but would be -k using the labelling on the juju site you linked. Either way it's a singularity. That's not a problem for the path homotopy, but it may well be for the integral.

You can calculate the integral around the singularity point using the same technique above of integrating along lines of constant $\alpha$ and constant $\phi$. You may need to break each of the four edges of the 'rectangle' into two, as each edge will traverse the images of two different quadrants of the zeta plane.

 

[aheight]

On your diagram the blue-green path is not a figure eight but looks like a simple closed curve that is path-homotopic to a point. However to collapse it homotopically to a point will require moving it to or over the singularity point which you have labelled as 1 on your diagram but would be -k using the labelling on the juju site you linked. Either way it's a singularity. That's not a problem for the path homotopy, but it may well be for the integral.

You can calculate the integral around the singularity point using the same technique above of integrating along lines of constant $\alpha$ and constant $\phi$. You may need to break each of the four edges of the 'rectangle' into two, as each edge will traverse the images of two different quadrants of the zeta plane.

Hi Andrew

I meant a figure-8 contour over the z-plane wrapping around the singular points 1 and k:

I was asking how is the contour mapped to the torus if the path is along an analytically-continuous route through the function $f(z)=\frac{1}{\sqrt{(1-z^2)(k^2-z^2)}}$.

 

[andrewkirk]

Is that graph drawn using the Schwarz-Christoffel formulas, or is it just drawn to be a figure eight, as a speculation that it might be the pre-image of the path?

Looking at your diagram in post 14, I would expect the path in the zeta plane to look like the attached diagram. If that's right then it looks like the only point the curve goes around is $\zeta(k)$. I don't currently have an intuition about the mapping from the complex plane to the rectangle, but I would have thought the pre-image of the path in the complex plane would be a line that comes down and right from upper-left, bounces off the real axis between -k and -1, heads off left and up to infinity, asymptotically approaching the imaginary axis, then it returns downwards and rightwards on the right side of the I am axis, bounces off the real axis between 1 and k then heads off up and rightwards to infinity again. It would not actually encircle any of the four singularity points.

 

[aheight]

Hi Andrew,
That's not what I have. Also, my diagram above goes around 1 and k and you are going around -k. The plot below shows what I have where I have color-coded the figure 8 contour as the thick red, blue, green, and yellow contours as it wraps around the surfaces of $\frac{1}{\sqrt{(1-z^2)(k^2-z^2)}}$ via Schwarz-Christoffel. Keep in mind there are two distinct paths around the the function since it's double-valued. My choice of starting point gives the plot in the zeta plane below. Can you see what the final contour looks like if I first bend the color plot along the $\xi$ axis first into a tube, then bend the tube into a torus towards the back of the plot so that the point -1 is facing us? It's not at all apparent to me. I had to actually map it to the torus to see what happens and the results are surprising.

 

[andrewkirk]

Yes mine had a mistake. It was with a torus that had the infinity points on the outer rather than the inner rim (bending the cylinder formed from the zeta square forwards to paste the left and right edges, rather than backwards).

But I cannot reconcile yours with the path shown in post 14 either. If we traverse that path in the direction such that we travel from green to blue rather than v.v, the path always exits by the side of the quadrant it's in that is to the left of the side by which it entered. That is, the path always turns left. Also, the path never traverses a side that has an infinity point on it. In your latest post, the path turns left and right alternately, and twice traverses a side with infinity on it.

I am currently thinking the path is like this:

It looks like my path just goes around $\zeta(1)$ so that its pre-image in the complex plane will be a simple, closed curve that does not self-intersect, whereas yours goes around $\zeta(1)$ and $\zeta(k)$.

 

[aheight]

Hi Andrew, that contour in post 14 is not from the figure 8, rather just a residual contour I left in the picture of a contour that loops around the singular point z=1. Sorry for the confusion. The plot below is the figure-8 contour mapped to the torus. Notice how it loops entirely around the torus tube (you can just barely make out the red and yellow segments underneath the torus. I found it surprising how a figure-8 contour in the z-plane is "rectified" into a circular contour on the torus. And of course, all of these calculations are dependent upon taking an analytically-continuous route through the function branches and in this case a figure-8 route around 1 and k is a closed (non-intersecting) loop so not too surprising all the contour legs in the $\zeta$ plane connect into a likewise closed non-intersecting loop over the torus.