Calculating the current through this load resistor

[Bolter]

Homework Statement

Find current flowing in load resistor

Relevant Equations

V=IR

Hi everyone

I have drawn what I think what the setup should look like, and worked out the equivalent resistance of the parallel connected resistors

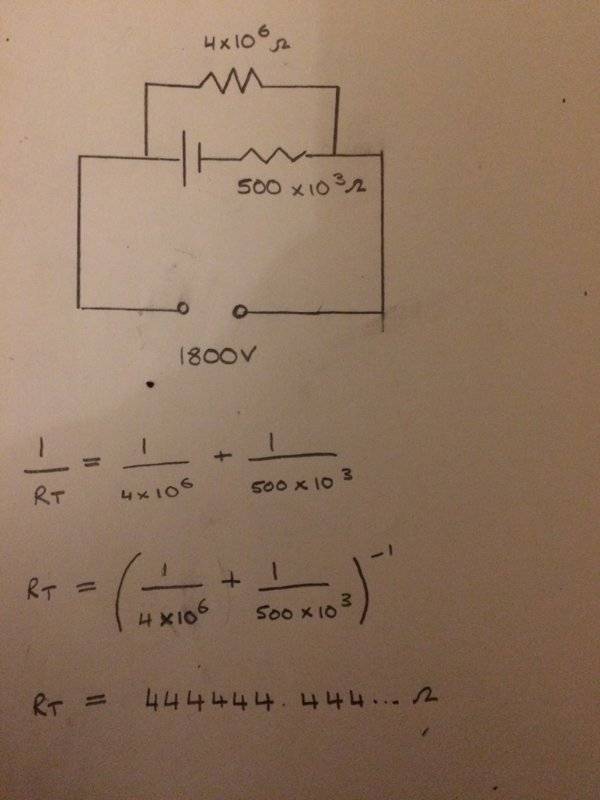
Not so sure where to go next with this problem?

Any help would be greatly appreciated!

 

[etotheipi]

I think you might have overcomplicated the setup slightly. The voltage source can be drawn in series with its internal resistance, and the two ends of this arrangement connect to the load resistor. Then it should be straightforward to calculate the current using Ohm's law.

 

[Bolter]

I think you might have overcomplicated the setup slightly. The voltage source can be drawn in series with its internal resistance, and the two ends of this arrangement connect to the load resistor. Then it should be straightforward to calculate the current using Ohm's law.

If so then then I have 2 resistors in series in the circuit. So the total resistance becomes 500,000 ohms + 4,000,000 ohms = 4,500,000 ohms

Giving I = V/R = 1800/4,500,000 = 0.0004 A or 0.4 mA?