InquisitiveOne
- 38
- 4
This isn't homework, I'm a hobbyist, not a student. Posting here because questions I've previously posted were moved to this section. My intent is to better understand humidity and it's role in compressed air for an automotive application. All help and direction is greatly appreciated. Thank you in advance.
A turbocharger compresses air which is then cooled, what is the new temperature?
How do I calculate the temperature of compressed air with different humidity values?
How do I calculate the volume or density of compressed air with different humidity values?
Atmospheric pressure - 14.7
Atmospheric air temperature - 77°F
Relative Humidity - 77%
Compressor efficiency - 60%
Compressed air cooler efficiency - 80%
Compressed air cooler media (water) temperature- 70°F
Air compressed to - 14.7psig/29.4psia/2bar
I haven't any idea where to start.
Pretty sure I've figured out how to accurately calculate for dry air, where using the following method and values above result in a temperature of 110.62°F and a volume of 0.53 it's original with 0% humidity:
Solving for temperature
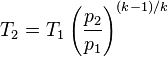
(k) 1.4 -1 = 0.4 / 1.4 = 0.286
(T1) 77°F + 459.69 = 536.69°Ra
(P1) 14.7psia
(P2) 29.4psia
T2= 654.36°Ra - 459.69 = 194.67°F
-----------
CE - Compressor Efficiency = 60%
T3 = (T2 - T1) / CE + T1
(654.36-536.69) / 0.60 + 536.69 = 732.81°Ra or T3 = 273.1°F
-----------
HE - Cooler efficiency - 80%
WT - Cooler media (water) temperature - 70°F (529.69°Ra)
T4 = T3 - ((T3 - WT) * HE)
732.81 - ((732.81-529.69) * 0.80)
732.81 - 162.50 = 570.31°Ra T4 = 110.62°F
----------
Solving for volume or compression ratio
CR = T1 / T2 x PR
Using T1, T4 and pressure ratio of 2 from above...
536.69 / 570.31 x 2 = 1.88:1 Compression Ratio
1 / 1.88 = 0.53
So, what was 1 cubic foot of 77°F air should now be 0.53 cubic feet and 110.62°F
Any links or insight on how to account for humidity and the effects of latent heat is very much appreciated.
Thank you again.
Homework Statement
A turbocharger compresses air which is then cooled, what is the new temperature?
How do I calculate the temperature of compressed air with different humidity values?
How do I calculate the volume or density of compressed air with different humidity values?
Atmospheric pressure - 14.7
Atmospheric air temperature - 77°F
Relative Humidity - 77%
Compressor efficiency - 60%
Compressed air cooler efficiency - 80%
Compressed air cooler media (water) temperature- 70°F
Air compressed to - 14.7psig/29.4psia/2bar
Homework Equations
I haven't any idea where to start.
The Attempt at a Solution
Pretty sure I've figured out how to accurately calculate for dry air, where using the following method and values above result in a temperature of 110.62°F and a volume of 0.53 it's original with 0% humidity:
Solving for temperature
(k) 1.4 -1 = 0.4 / 1.4 = 0.286
(T1) 77°F + 459.69 = 536.69°Ra
(P1) 14.7psia
(P2) 29.4psia
T2= 654.36°Ra - 459.69 = 194.67°F
-----------
CE - Compressor Efficiency = 60%
T3 = (T2 - T1) / CE + T1
(654.36-536.69) / 0.60 + 536.69 = 732.81°Ra or T3 = 273.1°F
-----------
HE - Cooler efficiency - 80%
WT - Cooler media (water) temperature - 70°F (529.69°Ra)
T4 = T3 - ((T3 - WT) * HE)
732.81 - ((732.81-529.69) * 0.80)
732.81 - 162.50 = 570.31°Ra T4 = 110.62°F
----------
Solving for volume or compression ratio
CR = T1 / T2 x PR
Using T1, T4 and pressure ratio of 2 from above...
536.69 / 570.31 x 2 = 1.88:1 Compression Ratio
1 / 1.88 = 0.53
So, what was 1 cubic foot of 77°F air should now be 0.53 cubic feet and 110.62°F
Any links or insight on how to account for humidity and the effects of latent heat is very much appreciated.
Thank you again.
Last edited: