Calculating the shear force of an impeller on cement mixture

[physicophile]

Hello All,

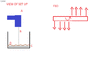
I have a quick question for you. I have small sample of a cement-like-like-material and I am high shear mixing it using a power drill and a impeller blade. The material is placed a beaker and the impeller blade shears the cement of the bottom of the beaker. I would like to calculate the amount of shear I am imparting upon the cement while I am mixing it.

The impeller is shaped like a upper case T

Please tell me if I am approaching my problem in the correct manner.

Shear = F/Area
Force = Mass*Acceleration
Acceleration = (v)^2/r
V=(w*r)
w= RPS/(2*PI)

Therefore the shear force on the cement is (\int mass *acceleration)/(area of impeller) = mass/(area of impeller)*\int ((w*r)^2/r) = mass/(area of impeller)\int (w^2*r^2)/r = w^2*mass/(area of impeller) \int r^2/r
= w^2*mass/(area of impeller) \int r = r^2*w^2*mass/(area of impeller)

The area of shear is the area of the bottom of the impeller in contact with the beaker, the cement is being mixed in.

Thank you very much for your help.

 

[nvn]

physicophile: I didn't check the whole post, but shouldn't w be rps*(2*pi), instead of rps/(2*pi)? What does rps mean in your post?

 

[physicophile]

Yes, you are right. Thanks for pointing that out to me. RPS = revolutions per second

 

[nvn]

physicophile: First, you say you have a quick question. Why do you think this is a quick question? Anyway, I am currently not understanding all of your parameters. Wouldn't you need to draw, and post, a good free-body diagram, with the dimensions and vectors labeled and shown? Some of your quantities are not defined nor explained. Why do you think mass is one lumped mass, instead of, e.g., dm = rho*b*t*dr? Why do you think area is one, big (undefined) area, instead of, e.g., dA = b*dr? Why do you think integral(r) = r^2, with no dr? Why do you think force is just mass times acceleration, when much of the force is caused by a distributed shear force? You list a parameter called "Force" and one called "F," but we never see either in the derivation. You also listed capital V and lowercase v. Two ambiguous names for the same thing? Or two different parameters? Also, you seem to be mixed up regarding radial acceleration. Radial acceleration does not cause shear force here.

 

[physicophile]

Please see attached pic for diagram set up and FBD


A= Power Drill – Contains a 8.5 AMP motor, No load speed of 3000 RPM. I do not know what the stall torque of the motor, nor do I have a motor toque /speed diagram

B= the impeller which is made of stainless steel. It has the following dimensions. Diameter = 2.300 inches, height of blade = 0.370, the width of blade = 0.10 inches. The mass of the impeller can be calculated using Mass= P*V=0.0056 kg/m^3 (assuming that p = 2700 kg/m^3 for AISI 304). The impeller is being scraped on the bottom of the mixing cup. I am physically pressing the cup into the impeller blade, so I am unsure of how much force the impeller blade is pressed into the cup with. If I had to guess I would say about 15 pounds.

C= Mixing Cup which has an diameter of 2.400 inches

D= Cement


“Why do you think mass is one lumped mass, instead of, e.g., dm = rho*b*t*dr? “
I am assuming the mass is the mass of the paddle blade shearing the mixture. This mass should not change. I the force acting upon my system in the x-y plane, therefore I was only taking the mass of the blade into consideration and am not factoring the force which I am pushing the bald into the mixing cup.

“ Why do you think integral(r) = r^2, with no dr?”
I did not add the dr because I forgot tothem into the equation.


As for the force, I was assuming the following.
Since I do not know the torque of my drill, I assumed the force acting upon the cement was
The angular acceleration of the blade times the mass of the blade. I thought that sense the mass of the blade was constant I did not have to use a double integral so I pulled it out of the equation.

 

[physicophile]

Please let me know if you need me to clairfiy my post further. I am in a hurry right now to get to work now, so I did not have the time to compose a very good FBD or answer your questions in great detail.

Your Help is greatly appreciate.

Thanks

 

[nvn]

physicophile: The angular velocity, w, is presumably constant. Therefore, the impeller mass is irrelevant. Integrate from zero to r1.

r1 = impeller radius = 29.21 mm = 0.029 21 m.
T = impeller shaft applied torque (N*m).
F1 = impeller shaft axial force = 67 N.
q1 = uniformly-distributed shear force on impeller due to cement viscosity and adhesion (N/m).
n1 = uniformly-distributed normal force on impeller due to pressing cup bottom against impeller (N/m) = F1/(2*r1).
mu = coefficient of friction between impeller and cup bottom.
q2 = uniformly-distributed shear force on impeller due to friction on cup bottom (N/m) = mu*n1 = 0.5*mu*F1/r1.

T = 2(q1 + q2)*integral(r*dr)
= 2(q1 + q2)(0.5*r1^2)
= (q1 + q2)*r1^2.

Unfortunately, I have no idea regarding the cement viscosity and adhesion; therefore, I have no idea regarding the value of q1. I also do not know the coefficient of friction, mu, for the impeller scraping against the cup bottom due to force F1. F1 is the normal force, due to you pressing the cup bottom against the impeller.

Perhaps the only way to obtain T is to attach some kind of torque measuring instrument between the impeller shaft and the power drill.