Calculating shear center for a "skewed" I beam

[greg_rack]

Homework Statement

Show that the horizontal distance of the shear center(SC) from the web is given by: $\xi_s=-d\frac{(d/h)^2sin\alpha cos\alpha}{1+6(d/h)+2(d/h)^3sin^2\alpha}$(picture of cross section(cs) below)

Relevant Equations

General shear flow equation: $q_s=-\frac{V_yI_{yy}-V_xI_{xy}}{I_{xx}I_{yy}-I_{xy}^2}\int_{0}^{s}tyds-\frac{V_xI_{xx}-V_yI_{xy}}{I_{xx}I_{yy}-I{xy}^2}\int_{0}^{s}txds+q_{s,0} \ \ \ \ \ \ \ \$ (1.1)

Here is the diagram of the cs:

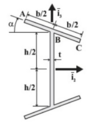
As a premise I must say that this topic(shear center and shear flow distributions) is still very hectic in my mind; I aim to clarify it a bit by asking you guys this :)
So, in order to identify the SC location, I must compute at what distance a point shear force must act so that it produces the same torque as the shear flow distribution; I'll pick this point to be the center of the web and call it H.
Let's thus assume the vertical shear force will act a distance $\xi_s$ to the left of H. I can therefore write:
$$V_y\xi_s=\sum{M_{qs}}$$
where $\sum{M_{qs}}$ is indeed the sum of all the contributions of the shear flow(sf) distributions to the internal torque about point H.
And now the fun begins... say I start by trying to determine the sf distribution in segment AB and segment CB defining a distance variable $s_1$ for the former, $s_2$ for the latter both going from the free edge "inwards".
Applying eqn (1.1) to flanges CB and AB yields(leaving 'y' indicated, as it's where the difference between the two lies):
$$q_{s}=-\frac{V_y}{I_{xx}}\int_{0}^{s_i}tyds$$
Working this out leaving 's' indicated, dividing by t and integrating both from 0 to b/2 should yield the total stress acting on the two flanges from which we can compute the force ultimately contributing to the integral torque, needed to solve for $\xi_s$.
But now all the questions arise:

• in order to succesfully apply eqn(1.1), should I know the direction of the shear flows beforehand? Otherwise, I wouldn't know how to manage the +/- signs; this really trips me off. For a vertical $V_y$ I would say the shear flow grows from 0 to a value both from C to be and from A to B, as for the "normal I beam" counterpart... but I am not sure; this is mere intuition. So is this equation limited for application to cases in which the sketch of the final distribution is already known?
• an year ago I attended a course on mechanics on material, in which the "shear formula" $\tau=\frac{VQ}{It}$ was derived and though a bit mysterious, was easy to use... but long story short a take away was that I couldn't fully rely on the equation: the distribution has to be more or less predicted, to check the numbers. Now, as (1.1) is the general case and the shear formula an approximation for a simple case, do the same "practical rules" apply when it comes to performing calculations on thin-walled sections?

These are only two of other doubts, hope to slowly start to clarify at least the main ones, and also hope I was clear.
Thank you in advance,

Greg

 

[member38644]

The process of calculating the shear center for a skewed I-beam can be complex, but it is an important step in analyzing the behavior of the beam under loading. The shear center is the point on the beam where a shear force can be applied without causing any twisting or bending. This is important because it allows us to accurately predict the behavior of the beam and design it accordingly.

To determine the shear center, we must first calculate the shear flow distribution along the beam. This can be done using the formula q = VQ/I, where V is the applied shear force, Q is the first moment of area of the section about the shear center, and I is the moment of inertia of the section about its centroid.

In order to apply this formula, we must know the direction of the shear flow at each point along the beam. This can be determined by considering the geometry of the beam and the direction of the applied shear force. For a vertical shear force, the shear flow will generally increase from the free edge towards the center of the beam.

However, in a skewed I-beam, the geometry is more complex and the shear flow may not be as straightforward. This is why it is important to carefully consider the geometry and direction of the shear force when determining the shear flow distribution.

In addition, the shear formula τ=VQ/It is an approximation that is valid for simple cases, but may not accurately represent the behavior of a skewed I-beam. Therefore, it is important to use the more general formula q = VQ/I to accurately determine the shear flow distribution and ultimately the shear center.

In summary, calculating the shear center for a skewed I-beam involves determining the shear flow distribution along the beam, which in turn requires careful consideration of the geometry and direction of the applied shear force. It is important to use the more general formula q = VQ/I to accurately determine the shear flow distribution and ultimately the shear center.