- #1
Rahulx084
- 99
- 1
1)In a flowing fluid in laminar fashion we know that it flows in planes which slides over each other, Let's take a fluid element (cylindrical) in a pipe(Radius=R) the resistive force is (stress)(cross section area of cylinder with radius 'r') acting in backward direction, now if I take Flow between two parallel fixed plates and I take a element(cubical with thickness dy and depth (inside screen) to be unity we see that the direction of stress on the top and bottom face of element is opposite. How we are determining the direction of the stress?
2)lets take a fluid slab in a pipe (flowing fluid in it), the difference in velocity of top and bottom plane of slab is du and thickness between them is dy , then we know stress= (viscocity) (du/dy), what does this stress mean and where this stress is acting , on top of slab or bottom of slab , in forward or backward direction?
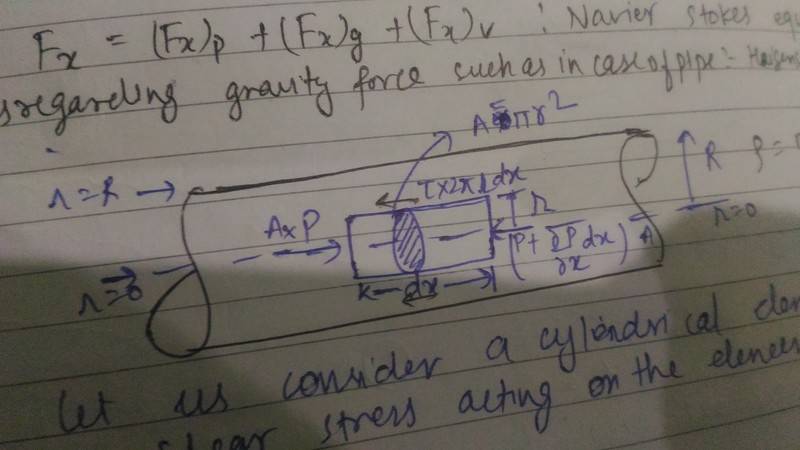

2)lets take a fluid slab in a pipe (flowing fluid in it), the difference in velocity of top and bottom plane of slab is du and thickness between them is dy , then we know stress= (viscocity) (du/dy), what does this stress mean and where this stress is acting , on top of slab or bottom of slab , in forward or backward direction?

