Calculating torsional stresses in welds that don't fit standard cases

In summary, the article discusses methods for calculating torsional stresses in welds that do not conform to standard cases. It emphasizes the importance of understanding the unique geometries and loading conditions of these welds to accurately assess stress distributions. The article presents alternative approaches and tools for engineers to analyze non-standard welds, ensuring safety and structural integrity in various applications.
  • #1
Kiblur
7
2
1716347393794.png


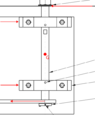
I was required to calculate the torsional stresses on these welds (in green) with the point of rotation G. However this doesn't fit any case in Shigley's so I'm at a loss as to how I should have calculated this. As advised by the teacher, I ended up replacing the keys being welded with full length keys so it would fit a case that I could use. However, that's just bad design. This isn't the first time I've had trouble calculating torsional stress because of an oddly shaped element. Below is another case I encountered. I would like to learn to calculate odd cases like this. Does anyone know of any resources that can help? Thank you very much.

1716347900938.png
 

Attachments

  • 1716347328126.png
    1716347328126.png
    7.7 KB · Views: 28
Physics news on Phys.org
  • #2
Kiblur said:
View attachment 345721
So you have the circumference indicated by the arrow in green welded and then torsion is applied there. I think you can approximate the stress at the welds with the torsion divided by the area of the weld. Another issue is how that torsion will travel through your part. I'd say the most critical section is the space in the middle where only two arms are supporting the load. The section there isn't a cylinder but comes from one. I feel like the results from the formula 3-36 from Shigley's should be somewhat precise.
$$\tau = \frac{T\rho}{J}$$
You'd need to calculate the polar moment of that section but that's doable without too much trouble because of the radial nature of the cross-section.
1716653033487.png

Of course, if you have the chance, correlate your hand-made results with FEA. Or even better, with experimental results.
 

FAQ: Calculating torsional stresses in welds that don't fit standard cases

1. What are torsional stresses, and why are they important in weld design?

Torsional stresses are the stresses that occur in a material when it is subjected to twisting or rotational forces. In weld design, understanding torsional stresses is crucial because they can lead to failure if the welds are not adequately designed to withstand these forces. Proper calculation of torsional stresses helps ensure the integrity and safety of welded structures, particularly in applications where they will experience twisting loads.

2. How can I calculate torsional stress in a non-standard weld configuration?

To calculate torsional stress in a non-standard weld configuration, you can use the general formula for torsional stress, which is τ = T*r/J, where τ is the shear stress, T is the applied torque, r is the distance from the center of the shaft to the point of interest, and J is the polar moment of inertia. For non-standard welds, you may need to determine the effective area and moment of inertia based on the geometry of the weld and the base materials involved.

3. What factors should I consider when evaluating welds subjected to torsional loads?

When evaluating welds subjected to torsional loads, consider factors such as the type of materials being welded, the geometry of the weld joint, the size and shape of the weld, the loading conditions (static or dynamic), and any potential stress concentrators. Additionally, the quality of the weld, including the presence of defects or discontinuities, should be assessed, as these can significantly affect the weld's ability to withstand torsional stresses.

4. Are there specific codes or standards for calculating torsional stresses in welded joints?

Yes, there are several codes and standards that provide guidelines for calculating torsional stresses in welded joints. Common standards include those from the American Welding Society (AWS), the American Institute of Steel Construction (AISC), and the American Society of Mechanical Engineers (ASME). These documents often contain methodologies for calculating stresses in various load conditions, including torsional loads, and can provide valuable insight into best practices for weld design.

5. How can I validate my calculations for torsional stresses in welds?

To validate your calculations for torsional stresses in welds, you can perform a combination of analytical methods, numerical simulations (such as Finite Element Analysis), and experimental testing. Comparing your analytical results with numerical simulations can help identify discrepancies and improve accuracy. Additionally, conducting physical tests on welded specimens under controlled conditions can provide empirical data to confirm your calculations, ensuring that the weld can safely withstand the predicted torsional stresses.

Similar threads

Stresses on a 3/16" fillet weld due to bending
Replies
3
Views
3K
Stress Analysis of Lifting Plate With Bail
Replies
1
Views
1K
Issues with SLS Model for Rubber and Foam Compression Tests
Replies
5
Views
473
Confidence in FEA stress values?
Replies
9
Views
2K
Calculating Axial Thrust for a Wheelchair Axle
Replies
4
Views
2K
How Can We Calculate the Fatigue Life of a Simply-Supported Beam?
Replies
6
Views
2K
Material choices and Stress Analysis for product im developing for school
Replies
1
Views
2K
Calculating Torsional Capacity of Square HSS
Replies
7
Views
25K
Stress analysis for a Bent Pipe
Replies
1
Views
6K
Residual stress - Ansys welding simulation
Replies
3
Views
5K

Hot Threads

Recent Insights

Back
Top