Calculating Velocity and Distance for Ascending Double Cone on Rails

[TSny]

Are the equations in post 27 right? Then the function v(d) and v'(d) appear very complicated...

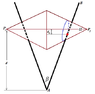
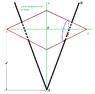
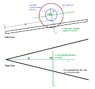
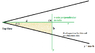
Yes, your expression for h looks good except for the overall sign. You want h to be a positive number.

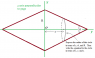
Your energy equation also looks good.

Your expression for r agrees with mine if you fix the overall sign of h. The expression for r will simplify somewhat.

 

[franceboy]

Thank you for your help.
What are your soulutions?
I got L=58.92cm and the maximal velocity is v(0.287m)=0.47m/s

There is also a part e) I have forgotten to post:
e) The assumption that the connecting line through the center of mass and the two pikes is always orthogonal to the rails is wrong. Analyse, where the rails really touch the double cone in the case of motion and find out what really happen in the point A.
I do not know how to deal with such kind of exercises... Could you give me some hints?

 

[TSny]

Yes, that's what I got except for a little round off difference. For d at max velocity I got 0.286 m and for the max velocity I got 0.464 m/s. I got exactly your answer for L.

I'll have to think about part (e).

 

[TSny]

Imagine a vertical plane that contains one of the rails. The plane will slice through the cone. The rail will contact the cone at the lowest point of the cross section. See the attached figure where you are looking at the cone along the axis connecting the apexes. For convenience, I drew the picture for the case where the plane of the rails is horizontal. The blue curve represents the cross section. The red dot shows the point of contact of the cone with the rail. You can see that the point of contact is offset from the apex by some distance $d_0$.

 

[franceboy]

Okay that means if d>0, the lines do not cross each other orthogonally. And d is zero if the double cone rolled a round, considered from the point A, right?

 

[TSny]

Okay that means if d>0, the lines do not cross each other orthogonally.

Yes, if you mean that line $P_1P_2$ is not orthogonal to the rail $AB$. If this is not what you mean, can you specify the lines that you are talking about?

And d is zero if the double cone rolled a round, considered from the point A, right?

I'm not sure I understand this question. If you work out the "offset distance" $d_0$ as a function of $d$, then I believe you will find that there must be some offset distance even at the starting point if you want the double-cone to rest on the rails at the starting point. So, the CM of the system would not actually be on a line through A and perpendicular to the plane of the rails at the starting point. Maybe this is what you are saying.

 

[franceboy]

I am talking about the line AB and the line through the center of mass and slice point from AB with the double cone.
Maybe this can be solved by vectors in the form
AB=(1,sin(y),tan(b/2)) Ocm(x,R+h,0) but I don not know how to describe OS, the slice point by the coordinate x of the center of mass.
With OS we could build the product AB*(Ocm-OS). The lines are orthogonal if this product is zero, isn't it?

 

[TSny]

To find the point where one of the rails touches the cone, find the equation for the conic section created by the intersection of the cone with a vertical plane containing the rail. This requires writing an equation for the surface of the cone and an equation for the vertical plane. Use these to find the equation for the intersection. You can express these equations relative to your coordinate system where the origin is at the center of mass of the cone, the x-axis passes through origin and is parallel to plane of rails, the y-axis runs along the axis of the double cone, and the z-axis is perpendicular to the plane of the rails. See diagram.

 

[franceboy]

I failed at describing the double cone with vectors and finding an intersection equation. Could you help me?

 

[TSny]

First find the equation for the cone in terms of the (x,y,z) coordinate system. Imagine the surface of the cone as made up of circular cross sections of varying radius.

 

[franceboy]

Sorry for answering so late.
Okay we imagine that the CM is the point CM=(x_CM, 0 , R+x_CM*(tan(y)-tan(b/2)*tan(a/2)).
Then the varying is dependent from the value of y. We can say: r=R-tan(a/2)*y_circle
The centre of the circle is (x_CM , y_circle , R+x_CM*(tan(y)-tan(b/2)*tan(a/2)). The circle is in the y-z-plane, therefore we have the circle equation: (y-y_circle)²+(z-( R+x_CM*(tan(y)-tan(b/2)*tan(a/2))²=r²
Moreover the rails can be described by: AB=t*(1 , tan(b/2) , sin(y))
What should I do next?

 

[TSny]

When the cone is at a certain position, I found it easier to choose the axes relative to the cone as shown. The x-axis runs through the CM of the cone and parallel to the rails. The equation for the circular cross section is then just x² + z² = r² where r is as given in your expression. You now have the equation for the surface of the cone in terms of x, y, and z.

Find an expression for the rail in the form y(x). This is also the equation for the plane that contains the rail and is parallel to the z axis. Use it in the equation for the cone so that you get a relation between x and z for the intersection of the the plane and the cone..

 

[franceboy]

Okay y(x) is supposed to be y(x)=tan(b/2)*x
And y(x)=y_circle Then we would have the equation:
(R-tan(a/2)*tan(b/2)*x)²=x²+z²
And z= root((R-tan(a/2)*tan(b/2)*x)²-x²)

 

[TSny]

Okay y(x) is supposed to be y(x)=tan(b/2)*x

The rail has a non-zero y-intercept in the chosen coordinate system.

 

[franceboy]

Is y(x)=tan(b/2)*x+R ?

 

[TSny]

Is y(x)=tan(b/2)*x+R ?

Not quite. y = tan($\small\beta /2$) x + b where b is the y-intercept as shown.

 

[franceboy]

Thanks.
Are my next attempts right?
How do I solve this task?

 

[TSny]

You have the right idea. Once you get the correct equation for intersection of the cone with the plane y = mx + b, you can then find the value of x that corresponds to the point where the cone touches the rail. Think about the value of dz/dx at this point.

 

[franceboy]

I was not able to find the equation for the intersection. Could you name this equation?
And what should I do after solving this equation?

 

[TSny]

The equation for the cone is of the form $x^2 + z^2 = r(y)^2$.

You already found the function $r(y)$ for the right hand side back in post #41.

The equation of the plane that passes through the rail and is parallel to the z -axis is of the from $y = mx + b$.

You need to find the values of $m$ and $b$ for the right hand side. I believe you have already found the correct value for $m$ in post #45.

$b$ is the y-intercept of the plane, where the y-axis is the axis of the cone that passes through the two apexes. You should be able to express $b$ in terms of $\beta$ and $d$. See the shaded triangle in the figure.

The intersection of the plane with the cone is found by substituting the plane equation into the cone equation.

 

[franceboy]

Thank you.
The function for the left rail is y=tan(b/2)*x+tan(b/2)*d . Then we have the equations x²+z²=r(y)²
The conclusion would be x²+z²=(R-tan(a/2)*(tan(b/2)*x+tan(b/2)*d))²
I think z can be expressed by z(x)=tan(y)*x+tan(y)*d.
Back to the exercise: How I find out where the rail touches the double cone? And what will happen at A?

 

[TSny]

The conclusion would be x²+z²=(R-tan(a/2)*(tan(b/2)*x+tan(b/2)*d))²

I think this is correct. This equation gives the projection into the x-z plane of the intersection of the cone and the plane (containing the rail and parallel to the z-axis). This intersection is the purple curve in the figure. There are a couple of ways you can try to find the point of contact of the rail and the cone:

1.) Note that the point of contact is the point where z takes on a maximum value on the purple curve. So, what is $dz/dx$ at the point of contact?

or

2.) Rearrange your equation for the intersection into the form $$\frac{(x+x_0)^2}{A^2} + \frac{z^2}{B^2} = 1$$ for certain constants $A$, $B$, and $x_0$. Interpret.

 

[franceboy]

Since z takes on it`s maximal value, z`(x)=0.
z(x)=root((R-tan(a/2)*(tan(b/2)*x+tan(b/2)*d))2 - x²)
I can solve the first equation with my calculator. Then I got the real x-value which differs from the x value of the center of mass.
What is the next step?