ProjectENIS
- 4
- 0
Homework Statement
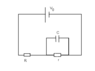
Given a circuit with two resistors, R and r, and a capacitor of C, and EMF of V0 as shown in the diagram, find the voltage across the capacitor during charging. Prove that this voltage, V is given by V = V0 (r/(R+r)) (1-e-((R+r)t)/(RrC))
Homework Equations
N.A.
The Attempt at a Solution
This is what I have
Loop A (with C): V0 + RI + q/c = 0 ==> I = (V0 - VC)/R
Loop B (with r): V0 + RI + rIr = 0
I = Ir + Ic ==> I = V/r + C(dv/dt)
From first and third,
(V0 - VC)/R = V/r + C(dv/dt)
Simplify to get,
V0 - RC(dv/dt) = V(1+R/r)
V = (r/[R+r])(V0 - RC(dV/dt))
The shape of the equation is getting there (I hope), but what do I do next? To get the given equation, RC(dV/dt) must be V0e-((R+r)t)/(RrC).
RC (dV/dt) = V, solving this differential equation to get ln (V) = -t/(RC) + k, hence, RC (dV/dt) = e-t/(RC) + k. And I am totally stuck.
Did I do something wrong somewhere? I can't think of anyway to get the RrC term in e-((R+r)t)/(RrC), not to mention the V0 and the (R+r) terms, unless k is like Rt/r. But that still does not give me a V0?