Calculating Water Velocity Using Bernoulli's Equation

Click For Summary

Homework Help Overview

The discussion revolves around calculating the velocity of water exiting an opening using Bernoulli's equation, and further exploring related questions about the motion of the water after it exits, including time to hit the ground, horizontal distance, and acceleration due to gravity.

Discussion Character

  • Exploratory, Conceptual clarification, Assumption checking

Approaches and Questions Raised

  • Participants discuss the application of Bernoulli's equation and question the use of conservation of energy and momentum in this context. They also consider the relevance of kinematic equations for analyzing the motion of the water after it exits the opening.

Discussion Status

Some participants have provided guidance on using conservation laws and kinematic equations, while others are exploring the implications of gravity on momentum conservation. There is an acknowledgment of missing visual context, which may affect the discussion.

Contextual Notes

Participants note the absence of a diagram initially, which is crucial for understanding the setup. There are also questions about specific values and parameters, such as the height (H) and the initial geometry of the setup.

Gamma
Messages
355
Reaction score
11
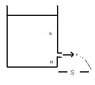
The velocity of the water that comes out of the opening in the attached diagram can be found using Bernoulli equation, as

v = sqrt (2gh)

Once the water exits the hole, I am not sure how to answer questions like the following: Can I use conservation of energy and momentum. Also can I use the equations in kinematics (ie. S = ut + 1/2 a t^2, v=u+at,...)

1. Time for the water to hit the ground,
2. What is the value of H
3. What is the horizontal distance of flight of water
4. What is the acceleration ( acce. of gravity??)


Thanks a lot.

Gamma.
 

Attachments

  • waterflow.JPG
    waterflow.JPG
    2.5 KB · Views: 457
Last edited:
Physics news on Phys.org
Usually the kinematic equations are all you need assuming you know the initial geometry of the set up. I see no picture, so I can't tell.
 
Yes the pic did not show up. It is there now. Sorry.
 
How about conservation of energy and momentum? I can cosider a mass of water that exits the hole per unit time as 'm' and write the conservation lows. Is seems ok to do that.

edit: May be momentum is not conserved in the vertical direction due to the force of gravity.?
 
Last edited:
You could use conservation laws also, I presume
 

Similar threads

How to calculate the velocity of water streaming into the boat?
  • · Replies 19 ·
Replies
19
Views
1K
Bernoulli’s Equation for plugging finger into dike under water
  • · Replies 4 ·
Replies
4
Views
2K
Bernoulli’s Equation and External Forces
  • · Replies 4 ·
Replies
4
Views
2K
What's the pressure long before the fluid exits a pipe?
  • · Replies 13 ·
Replies
13
Views
2K
Clarifying the Definition Total/Stagnation Pressure (p₀) in Bernoulli'
  • · Replies 2 ·
Replies
2
Views
1K
Bernoulli equation for calculation of water flow
  • · Replies 30 ·
2
Replies
30
Views
3K
Bernoulli equation / fluid flow / finding height
  • · Replies 6 ·
Replies
6
Views
3K
Formula derivation connecting vertical water flowrate & horizontal distance moved by a suspended sphere
  • · Replies 207 ·
7
Replies
207
Views
10K
Problem related to the Bernoulli Equation
  • · Replies 16 ·
Replies
16
Views
2K
Bernoulli's equation and water exit speed from tank opening
  • · Replies 29 ·
Replies
29
Views
5K