Calculation a reduced matrix element using E-Wigner Th.

[squareroot]

Hello.

I fail to follow one step in the process of calculating ⟨l_a∥Y^(L)∥l_b⟩ .

The spherical harmonics Y_ma^(L)(r) represent the 2L+1 components of the spherical tensor of rank L. Writing the Eckart-Wigner th. for M = 0 yields:

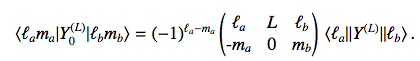(1)

Also one can write

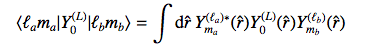(2)

Coupling L and l_b to l:

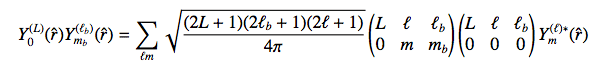(3)

Thus having

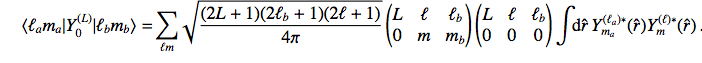(4)

Now solving the integral:

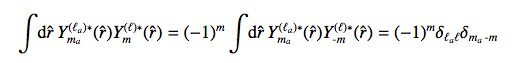(5)

So:

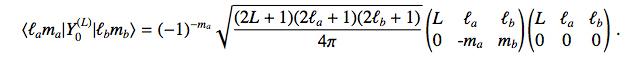(6)

Here is my problem! After solving the integral (5) and replacing it into (4) I don't understand how that changes the Wigner 3j symbols from

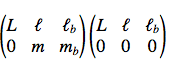(3) into

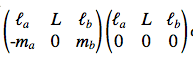(6)

Could anyone please help me with this step? I m guessing it has something to do with does kronecker deltas from solving the integral and they act on the wigner symbols after substitution... but i have no idea how!

 

[blue_leaf77]

In equation (4), the right hand side is summed over $l$ and $m$. However upon inserting the result from equation (5), only the term with $l=l_a$ and $m=-m_a$ survives. Yes it has to do with the property of Dirac delta symbol which is for any pair of integer $i$ and $j$, the Dirac delta $\delta_{ij}$ will give zero if $i\neq j$. If $i=j$, $\delta_{ij} = 1$.

 

[squareroot]

Oww i get it! Thank you so much!