sha1000
- 125
- 6
Hello,
I would like to calculate the orbital velocity using the geometrical way of reasoning. But I have a hard time to understand and apply some basics into my calculations.
The reasoning is pretty simple. After some time: dt ,the particle travels the distance: Vtot1 * dt = R*sinθ (see the attached image). In order to stay on orbit the velocity of the particle must change accordingly, by conserving the absolute value of the velocity and changing the velocity vector by θ.
Here is the problem that bothers me. Since the initial velocity Vtot1 = Vy is perpendicular to the center of the gravitational field, after time dt the orbital radius will increase from R to R+dR (see the attached image). In this case, it means that in order to stay on the orbit; the velocity Vtot2 must be different from Vtot1. Thus, it seems to me that this problem becomes more complicated.
- Does this reasoning make any sense?
- Are there any mistakes?
- Could you please guide me into solving this calculation. it's really important for me.
Sorry for my English.
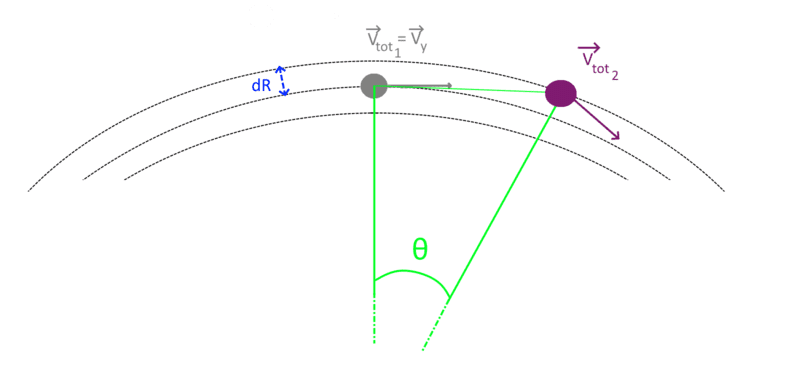
I would like to calculate the orbital velocity using the geometrical way of reasoning. But I have a hard time to understand and apply some basics into my calculations.
The reasoning is pretty simple. After some time: dt ,the particle travels the distance: Vtot1 * dt = R*sinθ (see the attached image). In order to stay on orbit the velocity of the particle must change accordingly, by conserving the absolute value of the velocity and changing the velocity vector by θ.
Here is the problem that bothers me. Since the initial velocity Vtot1 = Vy is perpendicular to the center of the gravitational field, after time dt the orbital radius will increase from R to R+dR (see the attached image). In this case, it means that in order to stay on the orbit; the velocity Vtot2 must be different from Vtot1. Thus, it seems to me that this problem becomes more complicated.
- Does this reasoning make any sense?
- Are there any mistakes?
- Could you please guide me into solving this calculation. it's really important for me.
Sorry for my English.