1LastTry
- 63
- 0
Calculus 2- Water pump problem
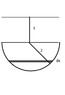
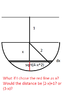
The lower half of a sphere with radius 2m is filled with water. Find the work needed to pump the water to a point 1m above the centre of the sphere.
I know you have to cut the problem into small pieces, and you have to label a "x" anywhere you want but you have to solve the problem based on which part you label the x (see attachment). But I have no idea where to label the x and how to get the integral with that information. And also what is the limits I put in the definite integral? I know it has to do with the x you choose but how to know which limit to use?
Homework Statement
The lower half of a sphere with radius 2m is filled with water. Find the work needed to pump the water to a point 1m above the centre of the sphere.
Homework Equations
The Attempt at a Solution
I know you have to cut the problem into small pieces, and you have to label a "x" anywhere you want but you have to solve the problem based on which part you label the x (see attachment). But I have no idea where to label the x and how to get the integral with that information. And also what is the limits I put in the definite integral? I know it has to do with the x you choose but how to know which limit to use?
Attachments
Last edited: