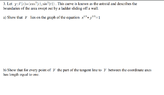Calculus III: Proving Tangent Line = 1 for Every Point on Curve

[Cactusguy21]

View attachment 8471

Hi, I'm stuck on a homework problem in my Calculus III class.

I solved 3a really easily, but 3b is giving me a lot of trouble. I know that to find the tangent line, I first have to find the slope, which is represented by the vector:

<3cos^2(t)(-sin(t)), 3sin^2(t)(cos(t))>.
I know the formula for arc length as well, although I don't think I necessarily would need this.

The formula for the tangent line should be:

r'(t)= <cos^3(t), sin^3(t)> + s<3cos^2(t)(-sin(t)), 3sin^2(t)(cos(t))>
where s is a parameter.

But how do I set it up so that I can prove the rest of the problem?

 

[Opalg]

Hi, I'm stuck on a homework problem in my Calculus III class.

I solved 3a really easily, but 3b is giving me a lot of trouble. I know that to find the tangent line, I first have to find the slope, which is represented by the vector:

<3cos^2(t)(-sin(t)), 3sin^2(t)(cos(t))>.
I know the formula for arc length as well, although I don't think I necessarily would need this.

The formula for the tangent line should be:

r'(t)= <cos^3(t), sin^3(t)> + s<3cos^2(t)(-sin(t)), 3sin^2(t)(cos(t))>
where s is a parameter.

But how do I set it up so that I can prove the rest of the problem?

Hi Cactusguy, and welcome to MHB!

What you have done so far is correct. Now find the equation of the tangent line in the form $y-y_0 = m(x-x_0)$, where $(x_0,y_0)$ is the point $(cos^3t,sin^3t)$ on the line, and $m$ is the slope, which from your calculation is $\dfrac{3\sin^2t\cos t}{-3\cos^2t(-\sin t)} = -\dfrac{\sin t}{\cos t}$. So the equation of the tangent line is \[y-sin^3t = -\frac{\sin t}{\cos t}(x - \cos^3t).\]

Simplify that equation, then put $y=0$ to find where it crosses the $x$-axis, put $x=0$ to find where it crosses the $y$-axis, and finally compute the distance between those points.