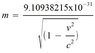QuantumCookie
- 2
- 0
Just a silly idea i have, please debunk it since i cannot figure it out:
The Thought Experiment:
Provided to us is a spacecraft equipped with a particle acceleration and detection systems.
The craft is set on a course where it would not be interrupted by any interstellar objects and cuts its propulsion systems for the entire duration of the experiment.
A stream of electrons are accelerated to a certain speed (let’s say 0.8c) in the particle accelerator. The mass of an electron in the stream is then measured when the electron stream passes, say, in the direction the spacecraft is traveling.
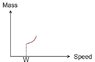
This measurement of electron mass when the electron stream passes in the direction the spacecraft is traveling is repeated for various speeds (0.82c, 0.84c, 0.86c, 0.88c and 0.9c). We then plot these values on a graph (e.g Figure 1). This graph represents the increase in mass of the electron at various velocities relative to the spacecraft .
(Figure 1)
The graph we obtained is then compared to the graph of:
(Figure 2a)
*9.10938215x10-31 kg is the rest mass of an electron
to see where it fits in. This can be achieved by comparing the change in gradients of both graphs. We then superimpose the graph we got (Figure 1) onto the graph of the equation of Figure 2a
(Figure 3)
We are now able to determine our velocity through spacetime in the direction the electron was traveling when it was measured by taking a point on the graph we obtained and subtracting the relative speed of the electron from its actual speed as reflected from the superimposed graph.
Example: In Figure 1, we measure the relative speed of the electron, W, to be say 0.8c. When we superimpose the graph, the point which contains W now reads off the new graph as X (lets say 0.83c), so we deduce that we are moving through spacetime at a velocity of 0.03c in the direction the electrons were traveling when their mass was measured.
This experiment is repeated where the mass of the electron is measured as it is traveling in various other directions to determine our absolute velocity through spacetime. The direction which yields the largest velocity will give us the absolute velocity of the spacecraft through spacetime.
Further Applications
The absolute velocity of the spacecraft through spacetime can be compared with the velocity of the spacecraft relative to the cosmic microwave background radiation (CMBR) reference frame.
If both velocities are the same, we can assume that the CMBR reference frame (and the black hole/object that gave birth to big bang) is/was moving at an absolute velocity of 0 m/s through space.
However, if both velocities were different, we can deduce that the CMBR reference frame (and the black hole/object that gave birth to big bang) is/was moving through space at a certain velocity.
This comparison would shed some light on the physical nature of the big bang itself, allowing us to eliminate a few of the seemingly infinite number of theories that surrounds the beginning of the universe we know today.
Thanks for reading!
The Thought Experiment:
Provided to us is a spacecraft equipped with a particle acceleration and detection systems.
The craft is set on a course where it would not be interrupted by any interstellar objects and cuts its propulsion systems for the entire duration of the experiment.
A stream of electrons are accelerated to a certain speed (let’s say 0.8c) in the particle accelerator. The mass of an electron in the stream is then measured when the electron stream passes, say, in the direction the spacecraft is traveling.
This measurement of electron mass when the electron stream passes in the direction the spacecraft is traveling is repeated for various speeds (0.82c, 0.84c, 0.86c, 0.88c and 0.9c). We then plot these values on a graph (e.g Figure 1). This graph represents the increase in mass of the electron at various velocities relative to the spacecraft .
(Figure 1)
The graph we obtained is then compared to the graph of:
(Figure 2a)
*9.10938215x10-31 kg is the rest mass of an electron
to see where it fits in. This can be achieved by comparing the change in gradients of both graphs. We then superimpose the graph we got (Figure 1) onto the graph of the equation of Figure 2a
(Figure 3)
We are now able to determine our velocity through spacetime in the direction the electron was traveling when it was measured by taking a point on the graph we obtained and subtracting the relative speed of the electron from its actual speed as reflected from the superimposed graph.
Example: In Figure 1, we measure the relative speed of the electron, W, to be say 0.8c. When we superimpose the graph, the point which contains W now reads off the new graph as X (lets say 0.83c), so we deduce that we are moving through spacetime at a velocity of 0.03c in the direction the electrons were traveling when their mass was measured.
This experiment is repeated where the mass of the electron is measured as it is traveling in various other directions to determine our absolute velocity through spacetime. The direction which yields the largest velocity will give us the absolute velocity of the spacecraft through spacetime.
Further Applications
The absolute velocity of the spacecraft through spacetime can be compared with the velocity of the spacecraft relative to the cosmic microwave background radiation (CMBR) reference frame.
If both velocities are the same, we can assume that the CMBR reference frame (and the black hole/object that gave birth to big bang) is/was moving at an absolute velocity of 0 m/s through space.
However, if both velocities were different, we can deduce that the CMBR reference frame (and the black hole/object that gave birth to big bang) is/was moving through space at a certain velocity.
This comparison would shed some light on the physical nature of the big bang itself, allowing us to eliminate a few of the seemingly infinite number of theories that surrounds the beginning of the universe we know today.
Thanks for reading!