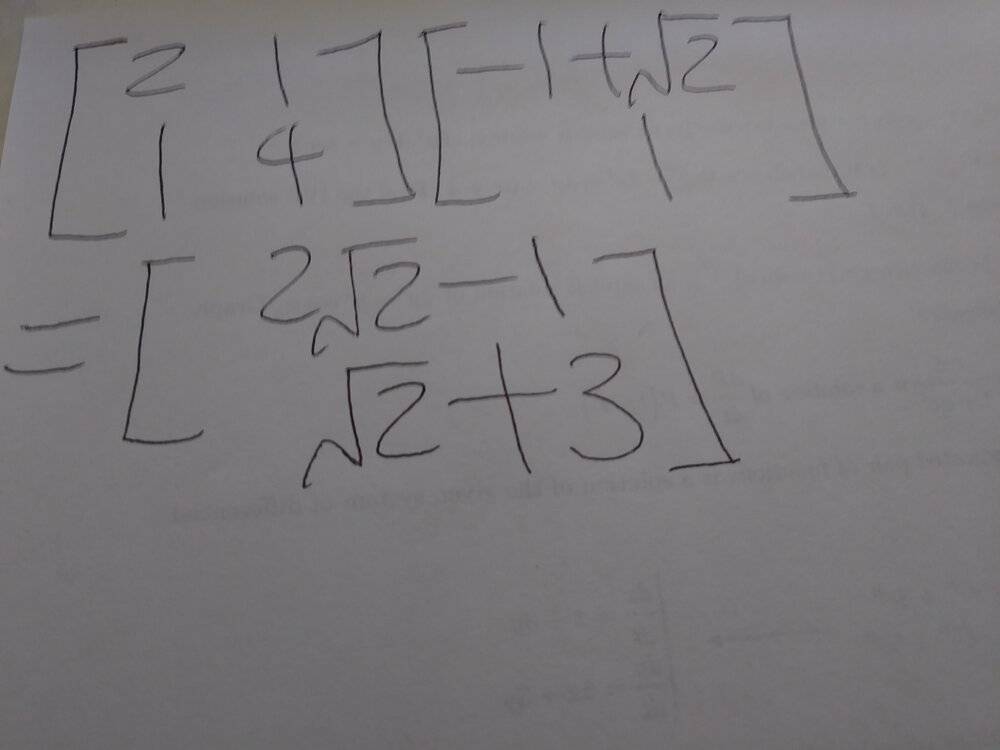SUMMARY
The discussion centers on determining whether a given vector is an eigenvector of another vector. The user initially answers "no" but later concludes that the vector
\(\begin{pmatrix} 2\sqrt{2} - 1\\ \sqrt{2} +3 \end{pmatrix}\) is indeed a scalar multiple of
\(\begin{pmatrix} \sqrt{2} - 1\\ 1 \end{pmatrix}\), confirming that it satisfies the eigenvector condition \(Av = \lambda v\). The correct answer is therefore "Yes," validating the user's final assessment.
PREREQUISITES
- Understanding of eigenvectors and eigenvalues
- Familiarity with vector notation and operations
- Knowledge of scalar multiplication in linear algebra
- Basic grasp of matrix transformations
NEXT STEPS
- Study the properties of eigenvectors and eigenvalues in linear algebra
- Learn about matrix transformations and their implications on vector spaces
- Explore the concept of scalar multiplication in depth
- Practice solving eigenvector problems using various examples
USEFUL FOR
Students of linear algebra, mathematicians, and anyone involved in vector space analysis will benefit from this discussion.