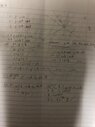Converting integration of rectangular integral to spherical.

[Eclair_de_XII]

Homework Statement

\begin{eqnarray}
0\leq z\leq \sqrt{x^2+y^2}\\
0\leq y\leq x\\
0\leq x\leq 1
\end{eqnarray}

$f(x,y,z)=\frac{(x^2+y^2)^\frac{3}{2}}{x^2+y^2+z^2}$

Relevant Equations

\begin{eqnarray}
x=\rho\cos\theta\cos\phi\\
y=\rho\sin\theta\cos\phi\\
z=\rho\sin\phi
\end{eqnarray}

Answer given in book: $\frac{\pi}{12}$
Answer derived: $\frac{3}{16}{\pi}$

I'm going to type out my LaTeX solution later on. But in the meantime, can anyone check my work? I know it's sloppy, disorganized, and skips far more steps than I care to count, but I'd very much appreciate it. I'm not getting the answer as given in the book. I think I failed this time because I assumed that $\phi$ was the angle from the x-axis (or any other axis that can be constructed with a line on the xy-plane) to some arbitrary point on the zx-plane. When I retried it while treating $\phi$ as the angle from the z-axis to some arbitrary point on the zx-plane, I got $\frac{3}{4}\pi(\frac{\pi}{8}-1)$. Can anyone point out anything I might have done wrong in the photograph I posted while I type out a LaTeX version of my second attempt? Thank you.

 

[Eclair_de_XII]

1 Convert rectangular bounds of integration into spherical bounds.
2 Convert $f$ to spherical form.
3 Integrate.

===1===

\begin{eqnarray}
x=\rho\cos\theta\sin\phi\\
y=\rho\sin\theta\sin\phi\\
z=\rho\cos\phi
\end{eqnarray}

\begin{eqnarray}
0\leq z\leq \sqrt{x^2+y^2}\\
0\leq y\leq x\\
0\leq x\leq 1
\end{eqnarray}

\begin{eqnarray}
x^2+y^2&=&(\rho\cos\theta\sin\phi)^2+(\rho\sin\theta\sin\phi)^2\\
&=&(\rho^2\cos^2\theta\sin^2\phi+\rho^2\sin^2\theta\sin^2\phi)\\
&=&\rho^2\sin^2\phi(\cos^2\theta+\sin^2\theta)\\
&=&\rho^2\sin^2\phi
\end{eqnarray}

\begin{eqnarray}
z=\sqrt{x^2+y^2}\\
\rho\cos\phi=\rho|\sin\phi|\\
\rho(\cos\phi-|\sin\phi|)=0
\end{eqnarray}

We're investigating a region in the first octant, so $\sin\phi>0$, and so $\phi=\frac{\pi}{4}$.

\begin{eqnarray}
z=0\\
\rho\cos\phi=0
\end{eqnarray}

Hence, $\phi=\frac{\pi}{2}$.

\begin{eqnarray}
y=x\\
\rho\sin\theta\sin\phi=\rho\cos\theta\sin\phi\\
\rho\sin\phi(\sin\theta-\cos\theta)=0
\end{eqnarray}

We are investigating the projection of the curve onto the xy-plane, so $\phi=\frac{\pi}{2}$, and so, $\theta=\frac{\pi}{4}$.

\begin{eqnarray}
y=0\\
\rho\sin\theta\sin\phi=0
\end{eqnarray}

Similarly, $\theta=0$.

It is given that $x\leq1$, and that $y\leq1$.
It is given also, that $z\leq\sqrt{x^2+y^2}\leq\sqrt{1^2+1^2}\leq\sqrt{2}$.

Hence, $x^2+y^2+z^2\leq1+1+2=4=2^2$, and so $\rho\leq2$.

Our spherical bounds are therefore:

\begin{eqnarray}
0\leq\rho\leq2\\
\frac{\pi}{4}\leq\phi\leq\frac{\pi}{2}\\
0\leq\theta\leq\frac{\pi}{4}
\end{eqnarray}

===2===

\begin{eqnarray}
f&=&\frac{(x^2+y^2)^{\frac{3}{2}}}{x^2+y^2+z^2}\\
&=&\frac{\rho^3\sin^3\phi}{\rho^2}\\
&=&\rho\sin^3\phi
\end{eqnarray}

===3===

\begin{eqnarray*}
\int_0^{\frac{\pi}{4}}\int_{\frac{\pi}{4}}^{\frac{\pi}{2}}\int_0^2(\rho\sin^3\phi)(\rho^2\sin\phi) d\rho d\phi d\theta&=&\int_0^{\frac{\pi}{4}}\int_{\frac{\pi}{4}}^{\frac{\pi}{2}}\int_0^2\rho^3\sin^4\phi d\rho d\phi d\theta\\
&=&\frac{1}{4}\rho^4|_0^2\cdot\frac{\pi}{4}\cdot\int (1-\cos^2\phi)^2 d\phi\\
&=&\frac{1}{4}2^4\cdot\frac{\pi}{4}\cdot\int(1-2\cos^2\phi+\cos^4\phi) d\phi\\
&=&\frac{1}{4}\cdot16\cdot\frac{\pi}{4}\cdot\left[\phi-\int(1+\cos2\phi) d\phi+\frac{1}{4}\int(1+\cos2\phi)^2 d\phi\right]\\
&=&4\cdot\frac{\pi}{4}\cdot[\phi-\phi-\sin2\phi+\frac{1}{4}\int(1+2\cos2\phi+\cos^2(2\phi))^2 d\phi]\\
&=&\pi\cdot\left[-\sin2\phi+\frac{1}{4}(\phi+\sin2\phi+\frac{1}{2}\phi+\frac{1}{4}\sin4\phi)\right]\\
&=&\pi\cdot\left[-\sin2\phi+\frac{1}{4}(\phi+\sin2\phi+\frac{1}{2}\phi+\frac{1}{4}\sin4\phi)\right]\\
&=&\pi\left[\frac{3}{8}\phi-\frac{3}{4}\sin2\phi+\frac{1}{16}\sin4\phi\right]|_{\frac{\pi}{4}}^{\frac{\pi}{2}}\\
&=&\frac{3}{4}\pi(\frac{\pi}{8}-1)
\end{eqnarray*}

 

[Delta2]

Sorry its a bit too hot here and I ll try to check your work later (cant give any promises though) but I tried this at wolfram and it seems to agree with the book
https://www.wolframalpha.com/input/...om+x=0+to+1,+y=0+to+x,+z=0+to+(x^2+y^2)^(1/2)

 

[Delta2]

One thing that confuses me is that you use $\theta$ for the azimuth angle and $\phi$ for the inclination angle, while I am used the other way around, but ok I ll try to overcome this.

 

[Delta2]

Section 2 looks correct
Section 3 doesn't look correct but even after I do the correction (wolfram says that $$\int \sin^4\phi d\phi=\frac{3}{8}\phi-\frac{1}{4}\sin2\phi+\frac{1}{32}\sin4\phi$$
i don't get the book answer.

SO you big mistake must be in correctly determining the spherical boundaries.

 

[Eclair_de_XII]

Okay, gotcha. I'll work on it. I very much suspect it's got something to do with the $\rho$ upper-bound.

It's got to rely on $\theta$ and $\phi$, I think.

 

[Eclair_de_XII]

Okay, so it turns out that this problem probably wanted me to use cylindrical coordinates, instead.

I cannot fathom how it can be done with spherical coordinates.

 

[Delta2]

Good that you did it in cylindrical coordinates and confirmed the book answer. (Cant check you work though cause no matter how much I tried to magnify it looks faint , I just can't make out all the symbols.)

When you find time post your work with cylindrical coordinates in Latex please.

 

[Eclair_de_XII]

I found the bounds for $r$ by looking at the projection of the surface onto the xy-plane. (See illustration in OP).

===1: Converting to cylindrical coordinates===

\begin{eqnarray}
x=1\\
r\cos\theta=1\\
r=\sec\theta
\end{eqnarray}

\begin{eqnarray}
0\leq r\leq \sec\theta\\
0\leq\theta\leq\frac{\pi}{4}\\
0\leq z\leq r
\end{eqnarray}

\begin{eqnarray}
f&=&\frac{(x^2+y^2)^\frac{3}{2}}{x^2+y^2+z^2}\\
&=&\frac{r^3}{r^2+z^2}
\end{eqnarray}

===2: Solving the integral===

\begin{eqnarray}
z=r\tan s\\
dz=r\sec^2 s\,ds\\
z^2+r^2=r^2\sec^2s\\
s&:&r\mapsto\frac{\pi}{4}\\
&:&0\mapsto0\\
\end{eqnarray}

\begin{eqnarray}
\int_0^\frac{\pi}{4}\int_0^{\sec\theta}\int_0^\frac{\pi}{4}\left(\frac{r^3}{r^2\sec^2s}\right)r(r\sec^2s\,ds)\,dr\,d\theta&=&\int_0^\frac{\pi}{4}\int_0^{\sec\theta}\int_0^\frac{\pi}{4}r^3\,ds\,dr\,d\theta\\
&=&s|_0^\frac{\pi}{4}\cdot\int_0^\frac{\pi}{4}\int_0^{\sec\theta}r^3\,dr\,d\theta\\
&=&\frac{\pi}{4}\cdot\frac{1}{4}\int_0^\frac{\pi}{4}\sec^4\theta\,d\theta\\
&=&\frac{\pi}{16}\cdot\int_0^\frac{\pi}{4}(1+\tan^2\theta)\sec^2\theta\,d\theta\\
&=&\frac{\pi}{16}\cdot\left(\tan\theta+\frac{1}{3}\tan^3\theta\right)|_0^\frac{\pi}{4}\\
&=&\frac{\pi}{16}\cdot\left(1+\frac{1}{3}\right)\\
&=&\frac{\pi}{16}\cdot\left(\frac{4}{3}\right)\\
&=&\frac{\pi}{12}
\end{eqnarray}

And I think it could be possible to solve this in spherical coordinates, if you set the upper bound of $\rho=\sec\theta\csc\phi$.

 

[Delta2]

Yes well this seems correct, initially I had my doubts about the boundaries for $\theta$ but after looking through some inequalities at wolfram (namely $0<\sin\theta<\cos\theta$) I think they are right.

I am not sure at all about the boundaries in spherical coordinates, to tell you the truth I am not so good in converting 3D domains between cartesian/spherical/cylindrical coordinates systems , that's why in my first post I checked first section 2 and 3 of yours.