- #1
miosim
- 140
- 0
Can a grandpa understand the Bell's Theorem?
Einstein said that you don't truly understand something unless you can explain it to your Grandma. I think that this should apply also to a grandpa.
I am a grandpa who is struggling to understand the Bell's Theorem. I read a number of popular books and articles, tryed Wikipedia, followed discussions on this forum, and even tried to read the original Bells’ paper, but I still cannot grasp the logic and the experimental proof of this theorem. The popular explanation of the experiment in terms of red and blue balls may be a good illustration but still doesn’t make sense to me as an explanation.
Of cause my inability to understand math is a biggest problem, but the controversial concepts of quantum mechanics don’t give me such a problem regardless that they are also based on math.
In spite of my shallow background in math (say high school level) I believe that this shouldn’t prohibit me to understand the physical concept assosiated with this theorem.
Actually, I view math as a formalized logic and logic works only within well defined area of knowledge. Therefore I am careful with the logical and mathematical deductions applied to subatomic events that are obviously not fully understood yet.
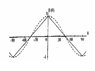
So I am asking for a help in understanding the Bell's theorem and its experimental proof in terms of physical concepts (of cause if we truly understand them). For the start I have a specific questions: How come the formalism of quantum theory leads to the Sine correlation while EPR formalism leads to Linear correlation (see Fig.below)?
Einstein said that you don't truly understand something unless you can explain it to your Grandma. I think that this should apply also to a grandpa.
I am a grandpa who is struggling to understand the Bell's Theorem. I read a number of popular books and articles, tryed Wikipedia, followed discussions on this forum, and even tried to read the original Bells’ paper, but I still cannot grasp the logic and the experimental proof of this theorem. The popular explanation of the experiment in terms of red and blue balls may be a good illustration but still doesn’t make sense to me as an explanation.
Of cause my inability to understand math is a biggest problem, but the controversial concepts of quantum mechanics don’t give me such a problem regardless that they are also based on math.
In spite of my shallow background in math (say high school level) I believe that this shouldn’t prohibit me to understand the physical concept assosiated with this theorem.
Actually, I view math as a formalized logic and logic works only within well defined area of knowledge. Therefore I am careful with the logical and mathematical deductions applied to subatomic events that are obviously not fully understood yet.
So I am asking for a help in understanding the Bell's theorem and its experimental proof in terms of physical concepts (of cause if we truly understand them). For the start I have a specific questions: How come the formalism of quantum theory leads to the Sine correlation while EPR formalism leads to Linear correlation (see Fig.below)?
Attachments
Last edited: