Can high school math prove this inequality?

[solakis1]

Using high school mathematics prove the following inequality:

$$\sqrt{a_{1}^2+...+a_{n}^2}\leq\sqrt{(a_{1}-b_{1})^2+...+(a_{n}-b_{n})^2}+\sqrt{b_{1}^2+...+b_{n}^2}$$

 

[lfdahl]

My attempt:

Spoiler

Squaring both sides:

\[\sum_{i}a_i^2\leq \sum_{i}(a_i-b_i)^2+\sum_{i}b_i^2+2\sqrt{\left ( \sum_{i}b_i^2 \right )\left ( \sum_{i}(a_i-b_i)^2\right )} \\\\ =\sum_{i}a_i^2+2\sum_{i}b_i^2-2\sum_{i}a_ib_i+2\sqrt{\left ( \sum_{i}b_i^2 \right )\left ( \sum_{i}(a_i-b_i)^2\right )} \\\\ \Rightarrow \sum_{i}a_ib_i -\sum_{i}b_i^2\leq \sqrt{\left ( \sum_{i}b_i^2 \right )\left ( \sum_{i}(a_i-b_i)^2\right )}\]

Squaring again:

\[\left ( \sum_{i}a_ib_i \right )^2+\left ( \sum_{i}b_i^2 \right )^2-2\left ( \sum_{i}a_ib_i \right )\left ( \sum_{i}b_i^2 \right )\leq \left ( \sum_{i}b_i^2 \right )\left ( \sum_{i}(a_i^2+b_i^2-2a_ib_i) \right ) \\\\ =\left ( \sum_{i}b_i^2 \right )\left ( \sum_{i}a_i^2 \right )+\left ( \sum_{i}b_i^2 \right )^2-2\left ( \sum_{i}a_ib_i \right )\left ( \sum_{i}b_i^2 \right ) \\\\ \Rightarrow \left ( \sum_{i}a_ib_i \right )^2\leq \left ( \sum_{i}a_i^2 \right )\left ( \sum_{i}b_i^2 \right )\]

This statement is the Cauchy-Schwarz inequality. Thus the stated inequality holds.

 

[solakis1]

My attempt:

Spoiler

Squaring both sides:

\[\sum_{i}a_i^2\leq \sum_{i}(a_i-b_i)^2+\sum_{i}b_i^2+2\sqrt{\left ( \sum_{i}b_i^2 \right )\left ( \sum_{i}(a_i-b_i)^2\right )} \\\\ =\sum_{i}a_i^2+2\sum_{i}b_i^2-2\sum_{i}a_ib_i+2\sqrt{\left ( \sum_{i}b_i^2 \right )\left ( \sum_{i}(a_i-b_i)^2\right )} \\\\ \Rightarrow \sum_{i}a_ib_i -\sum_{i}b_i^2\leq \sqrt{\left ( \sum_{i}b_i^2 \right )\left ( \sum_{i}(a_i-b_i)^2\right )}\]

Squaring again:

\[\left ( \sum_{i}a_ib_i \right )^2+\left ( \sum_{i}b_i^2 \right )^2-2\left ( \sum_{i}a_ib_i \right )\left ( \sum_{i}b_i^2 \right )\leq \left ( \sum_{i}b_i^2 \right )\left ( \sum_{i}(a_i^2+b_i^2-2a_ib_i) \right ) \\\\ =\left ( \sum_{i}b_i^2 \right )\left ( \sum_{i}a_i^2 \right )+\left ( \sum_{i}b_i^2 \right )^2-2\left ( \sum_{i}a_ib_i \right )\left ( \sum_{i}b_i^2 \right ) \\\\ \Rightarrow \left ( \sum_{i}a_ib_i \right )^2\leq \left ( \sum_{i}a_i^2 \right )\left ( \sum_{i}b_i^2 \right )\]

This statement is the Cauchy-Schwarz inequality. Thus the stated inequality holds.

Yes,but summation and the Cauchy-Schwarz inequality are not high school mathematics.

How would you prove the CSB inequality using high school mathematics

 

[Dethrone]

If we let $a$ and $b$ be $n$ dimensional (euclidean) vectors, then your statement follows directly from the reverse triangle inequality, which is a high-school concept. Now if you're asking for the proof of the triangle inequality, since I'm lazy I'll just say it is geometrically intuitive.

 

[lfdahl]

Yes,but summation and the Cauchy-Schwarz inequality are not high school mathematics.

How would you prove the CSB inequality using high school mathematics

Good question! I´m afraid I cannot come up with a real high school solution then ...:(

 

[MarkFL]

Good question! I´m afraid I cannot come up with a real high school solution then ...:(

It will be interesting to see the OP's solution. :)

 

[Albert1]

Using high school mathematics prove the following inequality:

$$\sqrt{a_{1}^2+...+a_{n}^2}\leq\sqrt{(a_{1}-b_{1})^2+...+(a_{n}-b_{n})^2}+\sqrt{b_{1}^2+...+b_{n}^2}$$

my solution:

Spoiler

using inductive method
$\sqrt{a^2_1}=\left | a_1 \right |=\left | a_1-b_1+b_1 \right |\leq \left | a_1-b_1\right |+\left |b_1 \right |
=\sqrt{(a_1-b_1)^2}+\sqrt{(b_1)^2}$

n=1 is true
suppose n=n is true
$$\sqrt{a_{1}^2+...+a_{n}^2}\leq\sqrt{(a_{1}-b_{1})^2+...+(a_{n}-b_{n})^2}+\sqrt{b_{1}^2+...+b_{n}^2}$$
let $P={a_{1}^2+...+a_{n}^2},Q={(a_{1}^2-b_1)^2+...+(a_{n}-b_n)^2},R={b_{1}^2+...+b_{n}^2}$
that is $\sqrt P\leq \sqrt Q+\sqrt R$
for n=n+1
we will prove :$\sqrt {P+a^2_{n+1}}\leq\sqrt {Q+(a_{n+1}-b_{n+1})^2}+\sqrt {R+b^2_{n+1}}$
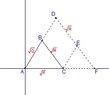
with the help of the following diagram it is easy to get the proof
here CF=$\sqrt {P+a^2_{n+1}}-\sqrt P$
BD=CE=$\sqrt {Q+(a_{n+1}-b_{n+1})^2}-\sqrt Q$
and BD//CE
BC=DE
and BC//DE
EF=$\sqrt {R+b^2_{n+1}}-\sqrt R$
that is $AF\leq AD+DF$
View attachment 6614
IF point D between A and F then equality will hold

 

[solakis1]

It will be interesting to see the OP's solution. :)

Spoiler

$$\sqrt{a_{1}^2+...+a_{n}^2}\leq\sqrt{(a_{1}-b_{1})^2+...+(a_{n}-b_{n})^2}+\sqrt{b_{1}^2+...+b_{n}^2}\Longleftrightarrow\sqrt{a_{1}^2+...+a_{n}^2}-\sqrt{b_{1}^2+...+b_{n}^2}\leq\sqrt{(a_{1}-b_{1})^2+...+(a_{n}-b_{n})^2}$$ .................1
And squaring and then cancelling equal terms we end up with:

$$\sqrt{(a_{1}^2+...a_{n}^2)(b_{1}^2+...b_{n}^2)}\geq(a_{1}b_{1}+...a_{n}b_{n})\Longleftrightarrow(a_{1}^2+...a_{n}^2)(b_{1}^2+...b_{n}^2)\geq(a_{1}b_{1}+...a_{n}b_{n})^2$$............2

Put :
$$A= a_{1}^2+...+a_{n}^2$$,

$$B= a_{1}b_{1}+...a_{n}b_{n}$$

$$C= b_{1}^2+...+b_{n}^2$$

Note: A and C are not zero

And (2) becomes:

$$AC\geq B^2\Longleftrightarrow AC-B^2\geq 0\Longleftrightarrow\frac{AC-B^2}{A}\geq 0\Longleftrightarrow A(x+\frac{B}{A})^2+\frac{AC-B^2}{A}\geq 0\Longleftrightarrow Ax^2+2Bx+C\geq 0\Longleftrightarrow (a_{1}^2+...a_{n}^2)x^2+2(a_{1}b_{1}+...a_{n}b_{n})x+ (b_{1}^2+...b_{n}^2)\geq 0$$$$\Longleftrightarrow (a_{1}x+b_{1})^2+...(a_{n}x+b_{n})^2\geq 0$$ which is true hence the intial inequality which is equivalent to the final one is also true

NOTE: $$\frac{AC-B^2}{A}\geq 0\Longrightarrow A(x+\frac{B}{A})^2+\frac{AC-B^2}{A}\geq 0$$ FOR ALL x's hence for x=-(B/A) WE have : $$ A(x+\frac{B}{A})^2+\frac{AC-B^2}{A}\geq 0\Longrightarrow\frac{AC-B^2}{A}\geq 0$$