- 11,326
- 8,754
It appears that you guys are having fun with this thread. Excuse me for jumping in late. It triggered memories. I played a lot with these things as a child. So much that I emptied my mother's sewing box of all her spare buttons. She got mad when she found out because for the first time in her life she had to go to the store and buy buttons. From those memories, I think I can point to the dominant energy loss in such a system and the exact likely failure location.
First, I believe that the dominant energy loss in the system is the bending and stretching of the fibers in the string/rope/cable. Think of the pulleys on a crane as in the picture below. It appears that the diameter of those pulley sheaves is about 15 inches. Why not smaller diameter? Because the smaller the diameter for bending, the greater the energy losses and the shorter the lifetime. Of course, the materials and braided/twisted structure, and the lubrication of the strands influence the quantitative results, but the qualitative statement that bending and stretching dominate energy losses remains true IMO. Twisting a bundle of strands necessarily bends and stretches.
 For failure mode, refer back to @OmCheeto 's diagram from #36.
For failure mode, refer back to @OmCheeto 's diagram from #36.
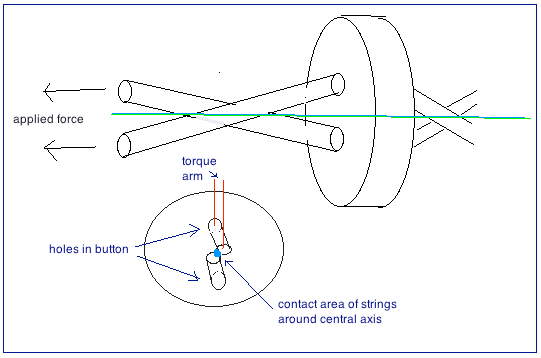
The holes in the button lie on a circle with radius ##R##. The strands (two strands in the diagram, but often 4 strands with buttons) form a twisted bundle with radius ##r##.
##r<<R##
At distance ##D## from the button on each side, the strands must depart from the bundle and fan out to go through the holes in the button. In @OmCheeto's diagrams ##D## is measured axially from the place where the strands cross to the button.
As ##D## approaches zero, further twisting becomes impossible and (at the final instant) nearly 100% of the inertial energy must go into stretching the strands in that tiny fan-out region. From my boyhood memories, failure occurs either when the strands break in the fan out region, or when the button fails as the strands cut through the material making the multiple holes merge into one hole in the center.
Thanks for sharing a topic fun for engineers.
First, I believe that the dominant energy loss in the system is the bending and stretching of the fibers in the string/rope/cable. Think of the pulleys on a crane as in the picture below. It appears that the diameter of those pulley sheaves is about 15 inches. Why not smaller diameter? Because the smaller the diameter for bending, the greater the energy losses and the shorter the lifetime. Of course, the materials and braided/twisted structure, and the lubrication of the strands influence the quantitative results, but the qualitative statement that bending and stretching dominate energy losses remains true IMO. Twisting a bundle of strands necessarily bends and stretches.
The holes in the button lie on a circle with radius ##R##. The strands (two strands in the diagram, but often 4 strands with buttons) form a twisted bundle with radius ##r##.
##r<<R##
At distance ##D## from the button on each side, the strands must depart from the bundle and fan out to go through the holes in the button. In @OmCheeto's diagrams ##D## is measured axially from the place where the strands cross to the button.
As ##D## approaches zero, further twisting becomes impossible and (at the final instant) nearly 100% of the inertial energy must go into stretching the strands in that tiny fan-out region. From my boyhood memories, failure occurs either when the strands break in the fan out region, or when the button fails as the strands cut through the material making the multiple holes merge into one hole in the center.
Thanks for sharing a topic fun for engineers.

 )
)


 But I had always struggled with great difficulty, any kind of advanced math.
But I had always struggled with great difficulty, any kind of advanced math.
