Can Polynomial Equations Be Solved Graphically?

[Erbil]

Hi.I'd like to ask a question about polynomal equations.
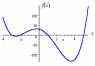
http://www.intmath.com/equations-of-higher-degree/1-polynomial-functions.php here is the solution polynomial function of degree 4. graphically.But I don't understand the method ? How we can use graphic method to solve? or can we use?

for example ; x^3+6x^2+15x+18

Can we solve this withous using the factorisation method.

 

[Simon Bridge]

Step 1: Use a computer program to plot the graph (pre-computers, we'd get good at guessing by plotting a few points.)
Step 2: using the mk1 eyeball, get approximate positions for the roots
Step 3: use a computer program to refine these approximations to some pre-specified accuracy.

the computer program will typically use the Newton-Raphson algorithm to refine the guess.

It is not really a graphical method - it is a numerical method.

 

[Erbil]

Understood :) I thought that they're usign the first and second derivative of a function to find the roots from graph.

 

[Erbil]

Understood :) I thought that they're usign the first and second derivative of a function to find the roots from graph.

I mean ;
http://en.wikipedia.org/wiki/Maxima_and_minima

 

[Simon Bridge]

Newton-Raphson uses the first derivative to refine guesses.
Graphically, you guess some value, take the tangent to f(x) at that value: where the tangent intercepts the x-axis will be closer to the root than the initial guess. Now take the tangent for that value: wash and repeat.

For instance - say we wanted to find the roots of $y=(x-1)^2$ by this method - let's illustrate the method by making a silly guess of x=4
That means y=9 ... no: not a root. The slope of the tangent is y'(4)=6 and the equation of the tangent is y=6x-15 so the intercept with the x-axis is x=15/6 which is closer to the actual root (x=1) than the initial guess.

The derivatives are only indirectly useful for finding the roots - you'll see the article you have referenced shows how to find and characterize the critical points.

See:
http://en.wikipedia.org/wiki/Newton's_method

 

[HallsofIvy]

You seem to be confusing a number of concepts. You cannot "solve" a polynomial such as $x^3+ 6x^2+ 15x+ 18$. You can solve a polynomial equation such as $x^3+ 6x^2+ 15x+ 18= 0$
There is a formula for solving cubic equations: look at the Cardano formula
http://www.sosmath.com/algebra/factor/fac11/fac11.html

There is a related formula for solving quartic (fourth degree) equations. It can be shown that there cannot be a similar formula for equations of degree 5 or higher because they can have roots that cannot be written in terms of roots and the other arithmetic operations.

 

[Simon Bridge]

I think he's just being sloppy about language.
The problem he wants to solve is of form "find the roots of..." - without factorizing.

<grizzle>
Did you see the webpage he linked to? ... it calls the factorization approach "the dinosaur method" and leaves it as a "if you really must"... favoring numerical methods instead.

OK it's chatty but how many people using the site have decided they don't need to be dinosaurs?
</grizzle>

I suppose, for completeness:
$y=x^3+6x^2+15x+18$ has one real root at $x=-3$
Hopefully we've covered all the bases - I'm sure Erbil can figure out how to use regression on complex numbers ... though this one is probably best done by quadratic equation now we know one root.

 

[Erbil]

I think he's just being sloppy about language.
The problem he wants to solve is of form "find the roots of..." - without factorizing.

<grizzle>
Did you see the webpage he linked to? ... it calls the factorization approach "the dinosaur method" and leaves it as a "if you really must"... favoring numerical methods instead.

OK it's chatty but how many people using the site have decided they don't need to be dinosaurs?
</grizzle>

I suppose, for completeness:
$y=x^3+6x^2+15x+18$ has one real root at $x=-3$
Hopefully we've covered all the bases - I'm sure Erbil can figure out how to use regression on complex numbers ... though this one is probably best done by quadratic equation now we know one root.

Yes,I mean is there any more practical way to do it?

You seem to be confusing a number of concepts. You cannot "solve" a polynomial such as x3+6x2+15x+18. You can solve a polynomial equation such as x3+6x2+15x+18=0

Yes,you're right.I'm talking about x3+6x2+15x+18=0 polynom equations.But not with cubic formula.

 

[Erbil]

Ok I have confused something. =) The web page that I linked is about polynomal functions.So functions can be graphed.But in my equation,only root can be graph.Because there's no depended variable to x.

There's the difference;
http://www.wolframalpha.com/input/?i=x^3+6x^2+15x+18=0 for roots,
http://www.wolframalpha.com/input/?i=f(x)=x^3+6x^2+15x+18 for function.

 

[Erbil]

ohh=) but in intmath.com he wrotes;

Finding the roots of an equation, for example

x4 − x3 − 19x2 − 11x + 31 = 0,

f(x) = x4 − x3 − 19x2 − 11x + 31

We see that there are 4 roots, at approximately

x = -3, x = -2, x = 1, x = 5.

 

[HallsofIvy]

I think he's just being sloppy about language.
The problem he wants to solve is of form "find the roots of..." - without factorizing.

<grizzle>
Did you see the webpage he linked to? ... it calls the factorization approach "the dinosaur method" and leaves it as a "if you really must"... favoring numerical methods instead.

Then whoever wrote that must really like dinosaurs! IF you can factor, then that is by far the best way to solve a polynomial equation. The only problem is that there are so few polynomials that you can factor.

OK it's chatty but how many people using the site have decided they don't need to be dinosaurs?
</grizzle>

I suppose, for completeness:
$y=x^3+6x^2+15x+18$ has one real root at $x=-3$
Hopefully we've covered all the bases - I'm sure Erbil can figure out how to use regression on complex numbers ... though this one is probably best done by quadratic equation now we know one root.

 

[Simon Bridge]

Which is the more practical method depends on the situation.
There is no "one best way".