- #1
iwantcalculus
- 15
- 1
The question is :
Show that the curve defined implicitly by the equation
X*Y^3 + x^3*Y = 4
has no horizontal tangent.The answer is :
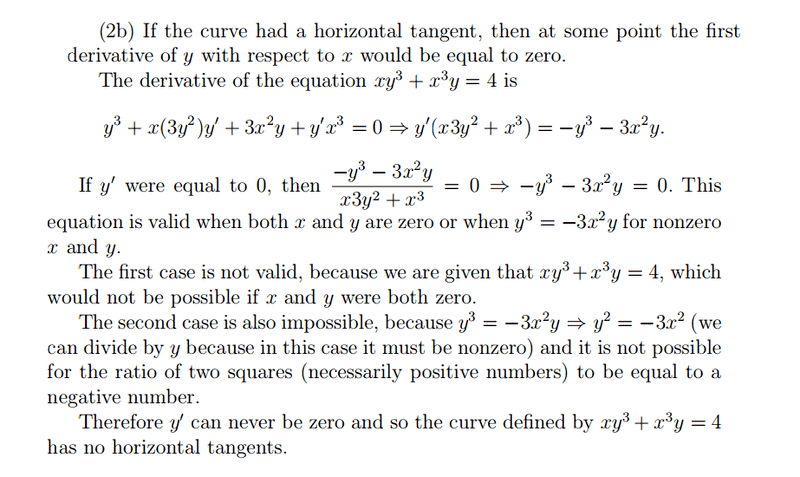 Can someone please explain what steps are used in order to obtain the answer in a simple way for a calculus beginner? This answer is not helping me understand the question and how to answer the question ( It is too complicated and gets me confused).
Can someone please explain what steps are used in order to obtain the answer in a simple way for a calculus beginner? This answer is not helping me understand the question and how to answer the question ( It is too complicated and gets me confused).
And if you have similar questions, please show me them so I can practice on them after I understand this question in order to be comfortable with this type of questions.
Show that the curve defined implicitly by the equation
X*Y^3 + x^3*Y = 4
has no horizontal tangent.The answer is :
And if you have similar questions, please show me them so I can practice on them after I understand this question in order to be comfortable with this type of questions.