Can someone help me find the angle between two forces?

[Blockade]

Can someone help me relearn finding the angle between two forces when solving for work of each forces (gravity, tension, f_F, normal)?
I remember that cos(90°-α) = sin(α) but what I don't understand is when the angle in between is "90°-α" or when it's just "α". I tried doing this on my own and but my work is always wrong when calculating the angle in between for each dot product.

Problem:

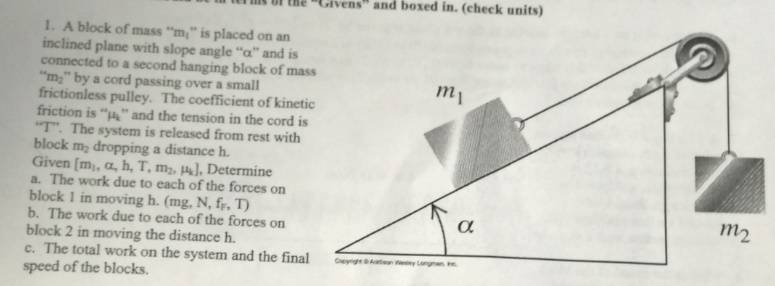
Attempt:

 

[haruspex]

I think you are asking how to check whether you should be using cos or sine of the given angle in the dot product.
A method I use to check that I have the right one is to think about an extreme case, such angle = 0. You know sin(0)=0 and cos(0)=1. Which value makes sense in the context?

 

[Blockade]

I think you are asking how to check whether you should be using cos or sine of the given angle in the dot product.
A method I use to check that I have the right one is to think about an extreme case, such angle = 0. You know sin(0)=0 and cos(0)=1. Which value makes sense in the context?

I have done some more work:

I think I got W_mg, W_T, and W_N correctly. However, I am still have difficulty finding the angle between the force of friction "μ_kcos(α)" and the displacement vector "h". The force of friction is suppose to be opposite from the displacement h for the block on the incline right? May you please check my 2nd attempt and see if my answers are correct?

W_fF = -μ_k*cos(α)*h , by the way since the angle between these two forces is 180° for the dot product.

 

[haruspex]

the force of friction "μ_kcos(α)"

That is not a force. What is missing?

 

[Blockade]

That is not a force. What is missing?

The mass and acceleration! "m₁g * μkcos(α)".

I have another question, for W_m1g, I am suppose to use m₁g or it cosine component: m₁g*cos(α) for F_m1g?

 

[haruspex]

for Wm1g, I am suppose to use m1g or it cosine component: m1g*cos(α) for Fm1g?

It depends how you are going to use it. What would you do to that to get the work?

 

[Blockade]

It depends how you are going to use it. What would you do to that to get the work?

Yes I would like to get work from it? So to get work should I use m₁g or m₁g*cos(α)?

 

[haruspex]

Yes I would like to get work from it? So to get work should I use m₁g or m₁g*cos(α)?

You did not answer my question. What will you do to or with the force, algebraically, to find the work?

 

[Blockade]

You did not answer my question. What will you do to or with the force, algebraically, to find the work?

Dot product the force of gravity and the displacement "h".

 

[haruspex]

Dot product the force of gravity and the displacement "h".

You can either find the force in the direction of h, making the dot product a simple multiplication, or take the force in its natural direction and apply the dot product rule when multiplying by the distance. It comes to the same answer either way.
However, it is not cos α you want here. Use the technique I mentioned: consider the case when α=0. Would there be any gravitational force on m₁ in the h direction?

 

[Blockade]

I think you are asking how to check whether you should be using cos or sine of the given angle in the dot product.
A method I use to check that I have the right one is to think about an extreme case, such angle = 0. You know sin(0)=0 and cos(0)=1. Which value makes sense in the context?

cos(0) = 1 since if you use sin(0)=0 your answer will always be 0?

 

[Blockade]

You can either find the force in the direction of h, making the dot product a simple multiplication, or take the force in its natural direction and apply the dot product rule when multiplying by the distance. It comes to the same answer either way.
However, it is not cos α you want here. Use the technique I mentioned: consider the case when α=0. Would there be any gravitational force on m₁ in the h direction?

Can you go more in depth with your technique? Right now I am using my best guess to answer your questions since I don't know where this is going. But to answer your question for Block m₁ there is force of gravity in the h direction and that force is m₁gsin(α)

 

[haruspex]

Block on m1 there is force of gravity in the h direction and that force is m1gsin(α)

Quite so. So what is the work done?

To check that it is sin, not cos, consider α=0. There is clearly now no force of gravity along the 'slope' (i.e. horizontal now), and sin(α)=0, so sin must be the right choice.

 

[Blockade]

Quite so. So what is the work done?

To check that it is sin, not cos, consider α=0. There is clearly now no force of gravity along the 'slope' (i.e. horizontal now), and sin(α)=0, so sin must be the right choice.

I am sorry, but what? So assume α = 0 so see if there are any forces left on the horizon? If so then sine is the right choice over cosine?

 

[haruspex]

I am sorry, but what? So assume α = 0 so see if there are any forces left on the horizon? If so then sine is the right choice over cosine?

When the angle is zero, the 'slope' is horizontal. In that situation, the force of gravity on m1 has no component along the slope, so cannot do any work along the the direction pf movement (h direction). It follows that the work is not mgh cos(α), since that would give mgh instead of 0.