- #1
ChiralSuperfields
- 1,206
- 132
- Homework Statement
- Please see below
- Relevant Equations
- Please see below
For part (c) of this problem,
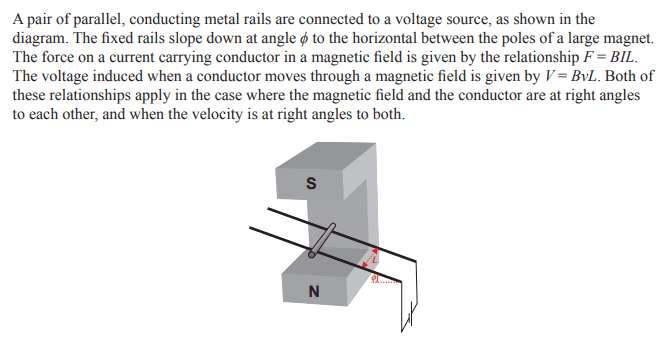
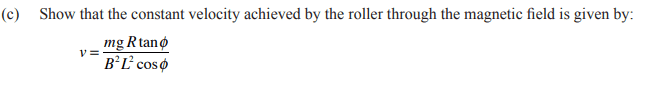
My working is
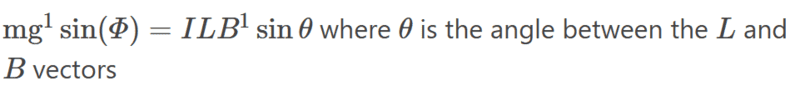
However, the tricky part is to find theta. I tried to draw the situation so that I could find theta:
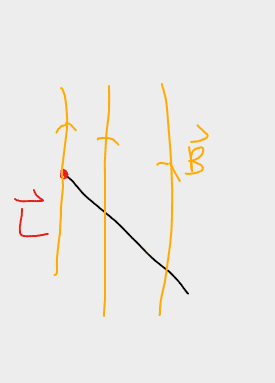
It appears that theta = 90 degrees. However, this does not seem to be correct. Does anybody please know how to correctly find theta in terms of phi?
Please note I am trying to do it in using the magnetic force cross product formula while the solutions find the components of perpendicular to each other then use the magnetic force formula that is only valid when the magnetic field, current and velocity are at right angles.
Thank you!
My working is
However, the tricky part is to find theta. I tried to draw the situation so that I could find theta:
It appears that theta = 90 degrees. However, this does not seem to be correct. Does anybody please know how to correctly find theta in terms of phi?
Please note I am trying to do it in using the magnetic force cross product formula while the solutions find the components of perpendicular to each other then use the magnetic force formula that is only valid when the magnetic field, current and velocity are at right angles.
Thank you!
