Rijad Hadzic
- 321
- 20
Homework Statement
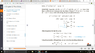
Attached is a picture..
the book went from
(-1 + \frac {2}{1+u} ) du + \frac {dx}{x} = 0
Edited by moderator.
to
-u + 2ln(1+u) + ln(x) = ln(c)
Homework Equations
The Attempt at a Solution
How in the world could the integral of 0 be ln(c)?
Maybe because it's 5 am and I'm up late and I'm hallucinating, but I always thought the integral of 0 is c, just a constant.
taking the integral of
(-1 \frac {2}{1+u} ) du + \frac {dx}{x} = 0
I get
(-u + 2 ln(u+1) + c ) + ln(x) + c_2 = c_3
-u +2ln(u+1) + ln(x) = c_4
Attachments
Last edited by a moderator: