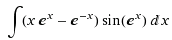SUMMARY
The integral discussed is solved using integration by parts, specifically involving the function e^x and trigonometric functions. The integral is expressed as I = ∫ ln(u) sin(u) du - ∫ (sin(u)/u²) du, where u = e^x. The final result is e - xsin(e^x) - xcos(e^x) + C, confirming the effectiveness of integration by parts in this context. Tools like Maple and Wolfram Alpha were utilized to verify the solution.
PREREQUISITES
- Understanding of integration techniques, specifically integration by parts.
- Familiarity with exponential functions and their properties.
- Knowledge of trigonometric functions and their integrals.
- Basic skills in using computational tools like Maple or Wolfram Alpha for verification.
NEXT STEPS
- Study the method of integration by parts in depth.
- Explore the properties and applications of exponential functions in calculus.
- Learn about the integration of trigonometric functions and their combinations.
- Practice using computational tools like Maple and Wolfram Alpha for solving complex integrals.
USEFUL FOR
Students, educators, and professionals in mathematics or engineering fields who are looking to enhance their skills in solving complex integrals and understanding advanced calculus techniques.