Can you me with this (it is all about vectors )

[donniemsb_12]

this example is being discussed by our professor in our class ! ( the one that i upload is the illustration made by our prof in our class )

this are the given and the solution :

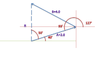
A=2.0m @ 40'
B=4.0m @127'

SOLUTION :

R^2=A^2+B^2– 2AB Cos93'
R^2=(2.0)^2 + (4.0)^2 -(2)(2)(4)cos93'
R=4.56m

sin⁡θ/4=sin93'/4.56 sin⁡θ=62.2'

11.2 west of north

guys ! please explain to me how did they get the sin⁡θ=62.2' and 11.2 west of north and the formula ! thanks ! if u answer this i can now make the assignment given by our prof thanks a lot !

 

[Doc Al]

What part don't you understand? Did you solve for sinθ? (That diagram is inaccurate, by the way.)

It's not sinθ = 62, but θ = 62. (approximately)

 

[donniemsb_12]

What part don't you understand? Did you solve for sinθ? (That diagram is inaccurate, by the way.)

It's not sinθ = 62, but θ = 62. (approximately)

that was being answered by our prof. that problem set as an example in our class ! ok please explain to me how did she get the answer of θ = 62' and the formula's ? and the " 11.2 west of north " where did it came from ? please help me thanks !

 

[Doc Al]

i don't know ! that was being answered by our prof. that problem set as an example in our class ! ok please explain to me how did she get the answer of θ = 62' and the formula's ? and the " 11.2 west of north " please help me thanks !

Look up the http://en.wikipedia.org/wiki/Law_of_sines" . That's how she got the formula.

And once you've solve for the angle in the triangle to be 61.2', then that's 11.2' past vertical, which is 11.2 west of north.

 

[donniemsb_12]

Look up the http://en.wikipedia.org/wiki/Law_of_sines" . That's how she got the formula.

And once you've solve for the angle in the triangle to be 61.2', then that's 11.2' past vertical, which is 11.2 west of north.

thanks sir ! now i know how did she get the 61.2 ! ! the thing that i don't know is the 11.2 west of north. please explain it more thanks !

 

[Doc Al]

thanks sir ! now i know how did she get the 61.2 ! ! the thing that i don't know is the 11.2 west of north. please explain it more thanks !

In the diagram, the resultant R makes an angle of 61.2 degrees with the vector A. Since vector A is at an angle of 40 degrees with the x-axis, that makes the resultant have an angle of 40 + 61.2 = 101.2 degrees. Which is 11.2 to the left of vertical (90 degrees). Which you can also describe as 11.2 west of north, if you take north as the +y axis.

 

[donniemsb_12]

In the diagram, the resultant R makes an angle of 61.2 degrees with the vector A. Since vector A is at an angle of 40 degrees with the x-axis, that makes the resultant have an angle of 40 + 61.2 = 101.2 degrees. Which is 11.2 to the left of vertical (90 degrees). Which you can also describe as 11.2 west of north, if you take north as the +y axis.

thanks ! i understand now ! that was a big help ! thank you so much ! can i ask more ? R^2=A^2+B^2– 2AB Cos(degree)' that formula ? is it always constant or it can be change base on the problem ?

 

[Doc Al]

thanks ! i understand now ! that was a big help ! thank you so much ! can i ask more ? R^2=A^2+B^2– 2AB Cos(degree)' that formula ? is it always constant or it can be change base on the problem ?

That's the http://en.wikipedia.org/wiki/Law_of_cosines" . It's a property of any triangle.

 

[donniemsb_12]

That's the http://en.wikipedia.org/wiki/Law_of_cosines" . It's a property of any triangle.

thanks sir ! last question sir ! in the 11.2 west of north ! how did the direction get ? the "WEST OF NORTH " ?

 

[Doc Al]

thanks sir ! last question sir ! in the 11.2 west of north ! how did the direction get ? the "WEST OF NORTH " ?

In the diagram, up is north and left is west. (So north is 90' from the x-axis.)

 

[donniemsb_12]

In the diagram, up is north and left is west. (So north is 90' from the x-axis.)

thanks sir ! ! ! now i understand this ! thank you very much ! god bless !