Can You Solve This Motion Problem Using a Simple Trick?

[bob012345]

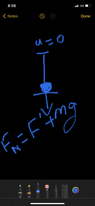
I got it @Steve4Physics If you ignore friction Then there is only one force. Due to this gravity it accelerates. And due to this acceleration there is a generation of another force. So there are actually two forces. Weight and the force due to acceleration.
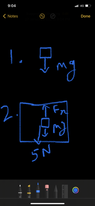
So F Net= 5N + W =5+2= 7 N.

It would be helpful for you to sketch a force diagram to see what is happening in the cardboard. This thread is keeping me on a knife-edge.

 

[rudransh verma]

You seem to be confusing yourself thoroughly. Certainly you are confusing me.

The 5 N you calculated in the first post is the net force. So the equation you write is

Yeah I calculated that. But to correct myself that is not Fnet. That is the force generated through acceleration. So net force will be this force + weight.

 

[bob012345]

Yeah I calculated that. But to correct myself that is not Fnet. That is the force generated through acceleration. So net force will be this force + weight.

Again, please draw the force diagram.

 

[rudransh verma]

Again, please draw the force diagram.

 

[bob012345]

There are two parts to this problem, each requiring a different force diagram. The first part is the free fall for 5M. The second part is when the knife is cutting through the cardboard. Force diagrams show ALL the forces, not just the net force. It will always help you in solving problems to get a clear understanding of what is happening before trying to calculate things.

 

[rudransh verma]

How does the value ‘’F=5N" (which you worked out in Post #1) relate to these two forces?

Fnet(friction)= 5N +weight

 

[bob012345]

Fnet(friction)= 5N +weight

What is the meaning of net force?

 

[Steve4Physics]

Thinking about the two forces on the knife while it cuts through the cardboard:
1) What is the direction of the knife's weight,W?
2) What is the direction of the resistive force on the knife, R?
3) What is the net (resultant) force acting on the knife in terms of W and R?
4) In your Post#1 calculation, which force did you find to be 5N?

Edit: typo's corrected.

 

[rudransh verma]

What is the meaning of net force?

Net force is the vector sum of all the forces

 

[kuruman]

The formal definition of the average of a function $F(q)$ taken over the interval $q_1 \leq q \leq q_2$ is $$\langle F \rangle_q=\frac{\int_{q_1}^{q_2}F(q)~dq}{\int_{q_1}^{q_2}dq}.$$This says that the $q$-averaged $F$ is the ratio of the area under the curve divided by the interval. This is equivalent to replacing the actual curve with a rectangle the height of which is $\langle F \rangle_q$ and has area equal to the integral (see figure below.)

This much is always the case when averaging. The question here is "what is $q$?
Case I: $q=t$
Starting with the numerator in the expression for the average, $$\begin{align}\int_1^2 F~dt=m\int_1^2 \frac{dv}{dt}~dt=m\int_1^2 dv=m(v_2-v_1)\implies \langle F \rangle_t=\frac{m(v_2-v_1)}{t_2-t_1}.\end{align}$$Case II: $q=x$
Starting with the numerator in the expression for the average, $$\begin{align}\int_1^2 F~dx & =m\int_1^2 {\frac{dv}{dt}~dx}=m\int_1^2 dv=m\int_1^2 \frac{dv}{dx}\frac{dx}{dt}~dx \nonumber \\ & =m\int_1^2v \frac{dv}{dx}~dx=m\int_1^2v~{dv}=\frac{1}{2}m(v_2^2-v_1^2)\implies \langle F \rangle_x=\frac{m(v_2^2-v_1^2)}{2(x_2-x_1)}.\end{align}$$Clearly, the two equations give different results in general. To find what must be true to get the same result, we set the two expressions for the average force equal:$$\frac{m(v_2-v_1)}{\Delta t}=\frac{m(v_2^2-v_1^2)}{2\Delta x}\implies \frac{\Delta x}{\Delta t}=\frac{v_2+v_1}{2}.$$This relation obtains when the acceleration is constant. Hence either equation (1) or (2) will give the correct (and same) result if the acceleration is constant.

I think that the two methods of averaging should be placed on an equal footing, i.e. there is no correct or incorrect or default way to find the average. If the acceleration is known to be constant, it makes no difference which expression is used. If the acceleration is not known to be constant, but can be assumed to be so, then again either expression works. If the acceleration is not constant and cannot be assumed to be so, e.g. a spring-mass system, the author of the question should specify explicitly the averaging method to be used or else the question is ambiguous.

 

[bob012345]

Net force is the vector sum of all the forces

Ok, but don't add the net force vector into the diagram also or you will always get confused. There are two forces acting on the knife while it is cutting through the cardboard.

 

[rudransh verma]

Thinking about the two forces on the knife while it cuts through the cardboard:
1) What is the direction of the knife's weight,W?
2) What is the direction of the resistive force on the knife, R?
3) What is the net (resultant) force acting on the knife in terms ofg W and R?
4) In your Post#1 calculation, which force did you find to e 5N?

1. Down
2. Up
3. F net = -W-5 =-2-5=-7
4. Force due to acceleration

 

[rudransh verma]

There are two forces acting on the knife while it is cutting through the cardboard.

Yeah! -W and -5 N(due to acceleration).

 

[bob012345]

Yeah! -W and -5 N(due to acceleration).

The labels may be confusing. In part one you used the kinematics formula assuming to get an acceleration and using the known distance you got a=25 $m/s^2$. You used that to get $F=5N$. That $F$ was the net force acting down. The question is what is the friction force acting up?

 

[rudransh verma]

The labels may be confusing. In part one you used the kinematics formula assuming to get an acceleration and using the known distance you got a=25 $m/s^2$. You used that to get $F=5N$. That $F$ was the net force acting down. The question is what is the friction force acting up?

7 N

 

[bob012345]

7 N

Yes, but do you understand why?

 

[rudransh verma]

I

Yes, but do you understand why?

said it many times. Force due to g at all time + force generated due to acceleration when dropped from some height.

 

[bob012345]

I

said it many times. Force due to g at all time + force generated due to acceleration when dropped from some height.

You said it many times but it is still not clear at all what you mean. The words force generated due to acceleration when dropped from some height does not sound like the force due to friction slowing the knife. Perhaps you mean there would be no friction if the knife weren't falling so gravity causes both forces but that is not a good way describe it. Better to simply say gravity acts on the knife at all times while friction resists the motion of the knife as it falls through the cardboard.

 

[jbriggs444]

Yeah I calculated that. But to correct myself that is not Fnet. That is the force generated through acceleration. So net force will be this force + weight.

$F_\text{net} = ma$

The force of friction, I would call the "force of friction". Thus avoiding confusion.

If you know $F_\text{net}$ because you have calculated acceleration then you can recover the force of friction by solving:$$F_\text{net} = F_\text{friction} + F_\text{gravity}$$ for $F_\text{friction}$

 

[rudransh verma]

You said it many times but it is still not clear at all what you mean. The words force generated due to acceleration when dropped from some height does not sound like the force due to friction slowing the knife. Perhaps you mean there would be no friction if the knife weren't falling so gravity causes both forces but that is not a good way describe it.

I am saying when you place your hand on the surface which force doyou apply. Weight! but when you throw your hand on the surface there is another force that is generated due to acceleration.

 

[bob012345]

I am saying when you place your hand on the surface which force do you apply. Weight! but when you throw your hand on the surface there is another force that is generated due to acceleration.

You do not apply weight. That is a very confusing way to think of it. Define another force that is generated due to acceleration. Acceleration of what? Having your own definitions and terms will get you into trouble with physics questions and it makes it difficult to help you.

 

[rudransh verma]

You do not apply weight. That is a very confusing way to think of it. Define another force that is generated due to acceleration. Acceleration of what? Having your own definitions and terms will get you into trouble with physics questions.

I mean its obvious. There is a force on the surface and that is W. IF you place your hand on surface does it break. Might not. But if you punch, then?

 

[jbriggs444]

I mean its obvious. There is a force on the surface and that is W.

As I use the term, "weight" (or "apparent weight") is the net inertial force resulting from gravity together with the choice of a particular rest frame.

My weight is a downward force on me. The force of my hand on a table is a separate force entirely. It is a contact force between my hand and the table.

When we "weigh" ourselves with a scale, we make use of Newton's second law. Since we are not accelerating, we can deduce that the supporting force from the scale (which the scale directly measures) matches the downward force from gravity (which the scale, thus, measures indirectly).

 

[bob012345]

I mean its obvious. There is a force on the surface and that is W. IF you place your hand on surface does it break. Might not. But if you punch, then?

It's obvious that if you hit something it might break but that is imprecise language to describe this physics problem.

 

[rudransh verma]

Better to simply say gravity acts on th eknife at all times while friction resists the motion of the knife as it falls through the cardboard.

Yes! Frictional force ${F_{fric}} = -(mg+force due to falling)= 7 N$.

 

[jbriggs444]

Yes! Frictional force ${F_{fric}} = -(mg+force due to falling)= 7 N$.

By "force due to falling", do you mean "total force required to explain the observed deceleration of the knife"?

 

[vela]

Forces are how pairs of objects interact. The weight is due to the interaction of the knife with the Earth. Friction is due to the interaction between the knife and cardboard. These two forces acting on the knife sum to produce a net force which results in the knife's acceleration.

In a sense, the discussion is about the language you're using, but your choice of words does seem to reveal a misunderstanding about forces. In particular, there is no force due to acceleration. Just because the knife is accelerating doesn't mean a third force is acting on the knife in addition to gravity and friction.

 

[bob012345]

Yes! Frictional force ${F_{fric}} = -(mg+force due to falling)= 7 N$.

The friction has nothing to do with falling. Calling it the force due to falling only adds confusion. It has to do with the kinetic energy the knife possesses as it hits the cardboard. That energy goes into ripping bonds as well as making heat and noise. In this case the kinetic energy comes about because the knife falls under the influence of gravity but the friction is not a force due to falling.

 

[Steve4Physics]

Yes! Frictional force ${F_{fric}} = -(mg+force due to falling)= 7 N$.

In what direction does this mysterious 'force due to falling' act?

If it is in the opposite direction to mg, your equation gives:
$F_{fric} = -(0.20\times10-5) = 3N$, not $7N$.

If it is in the same direction as mg, your equation gives:
$F_{fric} = -(0.20\times10+5) = -7N$, not $7N$.

Anyway, the expression 'force due to falling' is meaningless and highly confusing in this situation. You need to avoid it if you hope to be able to solve other problems of this sort.

There are only 2 forces acting on th knife as it cuts through the cardboard:
knife's weight (W)
resistive force of cardboard (R)
And their vector sum is $F_{net}$,

You need to work out how to answer the question using W, R and $F_{net}$.

 

[haruspex]

That is the important part, yes. But you have to divide by total distance, of course.

I think that's the $\Delta x$.