Capacitance and induced charge of a spherical Capacitor + dielectric

[titansarus]

Homework Statement

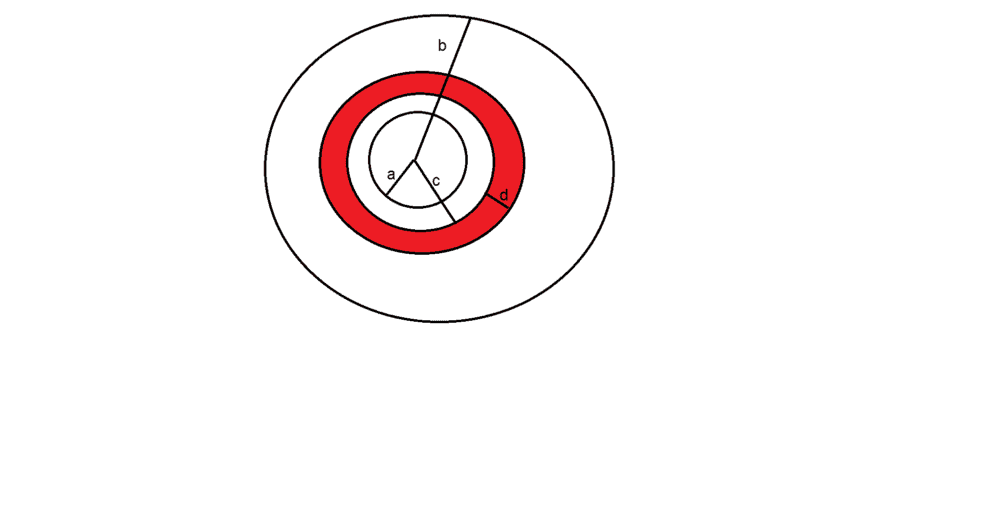
We have two conductor spherical shells with radius $a$ and $b$ with charges +Q and -Q and a dielectric $k$ with thickness $d$ is put in distance $c$ from the center. (As in the picture

I) Find the Capacitance of capacitor?

II) Find the induced charge inside dielectric in a position with radial distance$r$ where $c<r<c+d$

Relevant Equations

$C = Q/V , V =-\int E.ds$

I) For the first part I used:

$V = - \int E ds = \int_a^c \frac{1}{4\pi\epsilon_0} Q /r^2 dr+ \int_c^{c+d} \frac{1}{k} \frac{1}{4\pi\epsilon_0} Q /r^2 dr + \int_{c+d}^b \frac{1}{4\pi\epsilon_0} Q /r^2 dr$

And by using $C = Q/V$ We get an answer which is somehow large for writing here but It is just a bit of algebra after evaluating those integrals.

II) For this part I am not sure what should I use. If I say that $E_{in ~dielectric} = \frac{1}{k} E_{without~dielectric}$ We get $Q - Q' = Q/k$ where Q' is induced charge. But I am not sure is it safe to use this equation in this part? The answer isn't in terms of $r$ radial distance.

 

[rude man]

I) For the first part I used:

$V = - \int E ds = \int_a^c \frac{1}{4\pi\epsilon_0} Q /r^2 dr+ \int_c^{c+d} \frac{1}{k} \frac{1}{4\pi\epsilon_0} Q /r^2 dr + \int_{c+d}^b \frac{1}{4\pi\epsilon_0} Q /r^2 dr$

And by using $C = Q/V$ We get an answer which is somehow large for writing here but It is just a bit of algebra after evaluating those integrals.

II) For this part I am not sure what should I use. If I say that $E_{in ~dielectric} = \frac{1}{k} E_{without~dielectric}$ We get $Q - Q' = Q/k$ where Q' is induced charge. But I am not sure is it safe to use this equation in this part? The answer isn't in terms of $r$ radial distance.View attachment 242350

Where is the induced charge located in the dielectric? Does it make sense to expect variation with r?
EDIT: Use Gauss's law to determine where the induced charges reside. You know how E varies with k.