Capacitance Circuit - Voltage and Charge

[PerfPhys]

1. The Question
a. What is the equivalent capacitance of the combination shown in the figure ?
b. If a 100V battery is connected across the combination, what is the charge on each capacitor?
c. What is the voltage across each?

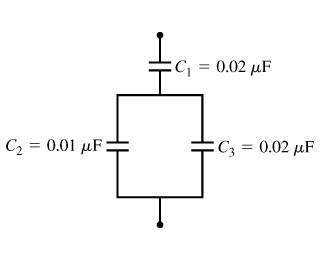
2. Equations
C=Q/V, adding capacitance rules

3. Solution attempt
For part a, I added C2 and C3 to get .03, then added the two in series (1/.02)+(1/.03) and took the inverse to get a combination capacitance of .012 microF

I am stuck on parts b and c, though. For B, we know Q=V/C and for C2 it would be Q=(100V)(0.01microfarads) which gives a charge of 1 microcoulomb.

for C3 it would be Q=(100V)(.02microfarads)=2 microcoulombs.
And for C1 it would be Q=(100V)(.02microF)= 2 microcoulombs.

However this answer is not working.

For part C, I tried plugging the charge and C into the same equation to get the V back out, but again this has not worked. I'm not sure if my units are off, or if I am missing something conceptually.[/b]

Any help would be appreciated!

 

[PerfPhys]

Nevermind, I just figured it out - I was trying to use the individual capacitance of C2 and C3 when I should have been using the combined since they are in parallel. :)

 

[tomcue]

Hello, thank you for your question. It seems like you are on the right track with your solution attempt. Let's take a closer look at parts b and c.

For part b, you correctly calculated the charge on each capacitor using Q=CV. However, the units for capacitance should be in Farads (F) and not microfarads (μF). So the charge on C2 would be 1 μC (microcoulomb) and on C3 and C1 it would be 2 μC.

For part c, you can use the equation V=Q/C to find the voltage across each capacitor. Again, make sure to use the correct units for capacitance. So for C2, the voltage would be 100V, for C3 and C1 it would be 50V each.

I hope this helps clarify the solution for you. Just remember to pay attention to the units and make sure they match up in your calculations. Good luck!