- 23,199
- 7,681
Homework Statement
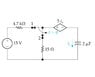
Select the correct expression for ##i_o(t)## for ##t≥0^+##.
Homework Equations
##V(t) = V(∞)+[v(0)-v(∞)]e^{\frac{-(t-t_0}{\tau}}##
##i(t) = C\frac{dV(t)}{dt}##
##\tau = RC##
The Attempt at a Solution
I'm a bit stuck on this problem. Specifically, I'm not sure how to deal with the dependent source.
At ##t=0##, the voltage of the capacitor should be 15 volts since the capacitor is directly in series with the voltage source with no branches leading off anywhere.
After ##t=0## the current through the capacitor would be ##C\frac{dV(t)}{dt}##, but I'm sure the dependent source changes things somehow. I'm just not sure how.