- #1
Xhendos
- 8
- 1
- Homework Statement
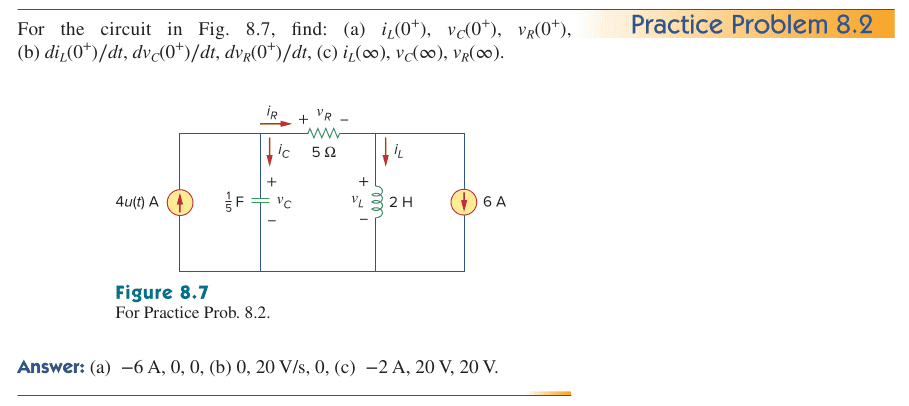
- For the circuit in Fig. 8.7, find: (a) i L (0 + ), v C (0 + ), v R (0 + ),
(b) di L (0 + )∕dt, dv C (0 + )∕dt, dv R (0 + )∕dt, (c) i L (∞), v C (∞), v R (∞).
- Relevant Equations
- I = C dv/dt
V = L di/dt
Dear PF,
I am trying to solve practice problem 8.2. I am stuggling with part B of the question which asks us to find diL(0+)/dt, dvC(0+)/dt and dvR(0+)/dt.
 My attempt can be seen below. Before t=0 the 4A current source is not present and thus it is an open circuit. A capacitor acts as an open circuit to DC and an inductor acts as a short circuit to steady-state DC conditions and thus that is why schematic for part A of the question looks like that. Using this schematic I find that iL = -6A and both vC and vR are 0V. This matches the answer of the book.
My attempt can be seen below. Before t=0 the 4A current source is not present and thus it is an open circuit. A capacitor acts as an open circuit to DC and an inductor acts as a short circuit to steady-state DC conditions and thus that is why schematic for part A of the question looks like that. Using this schematic I find that iL = -6A and both vC and vR are 0V. This matches the answer of the book.
However, for part B of the question, I did manage to find dv/dt by using KCL at node A and B and using the fact that the inductor cannot change its current abruptly, so for t = 0+ the inductor current is still -6A.
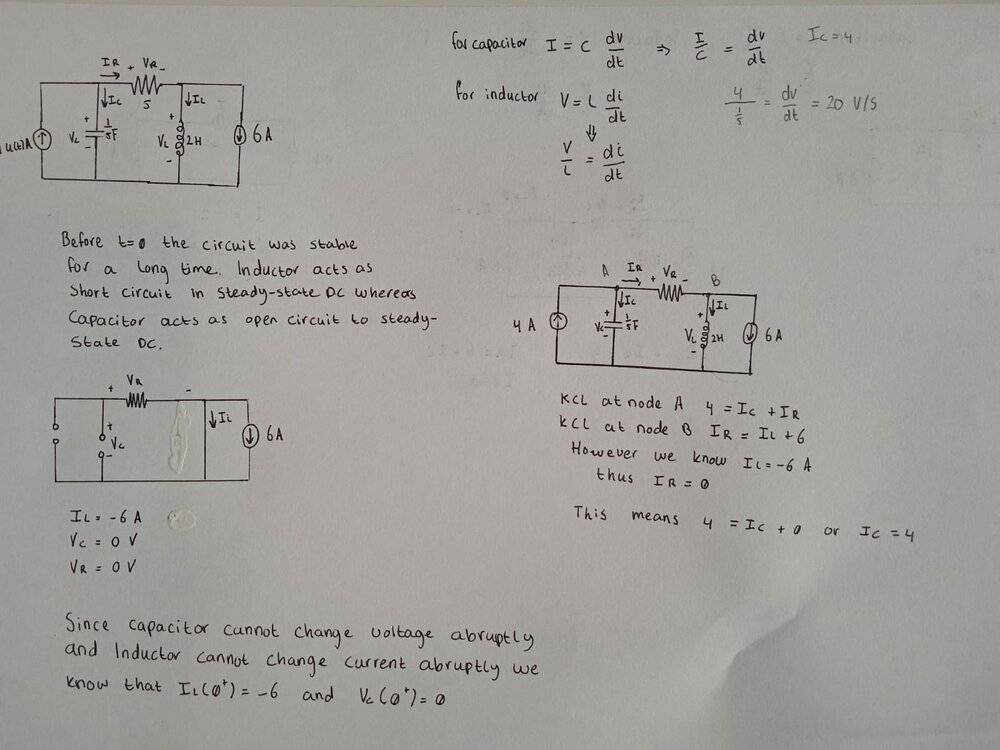
However, I am not quite sure how I can find di/dt and dr/dt. Can anyone give me a little hint here? I am stuck on this for quite a while.
I am trying to solve practice problem 8.2. I am stuggling with part B of the question which asks us to find diL(0+)/dt, dvC(0+)/dt and dvR(0+)/dt.
However, for part B of the question, I did manage to find dv/dt by using KCL at node A and B and using the fact that the inductor cannot change its current abruptly, so for t = 0+ the inductor current is still -6A.
However, I am not quite sure how I can find di/dt and dr/dt. Can anyone give me a little hint here? I am stuck on this for quite a while.