Step response of RC circuit with independent voltage and current sources

[Xhendos]

Homework Statement

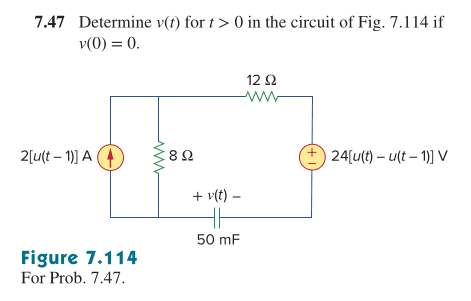
Determine v(t) for t > 0 in the circuit of Fig. 7.114 if
v(0) = 0

Relevant Equations

v(t) = Vs + (Vo - Vs) e^(-t/(RC))

Dear PF,

In the figure down below is Q7.47 which asks to determine the voltage v(t) across the capacitor for t > 0.
Since it is given that V(0) = 0 there are two scenario's which is between time interval 0 < t < 1 and t > 1 according to the independent sources.

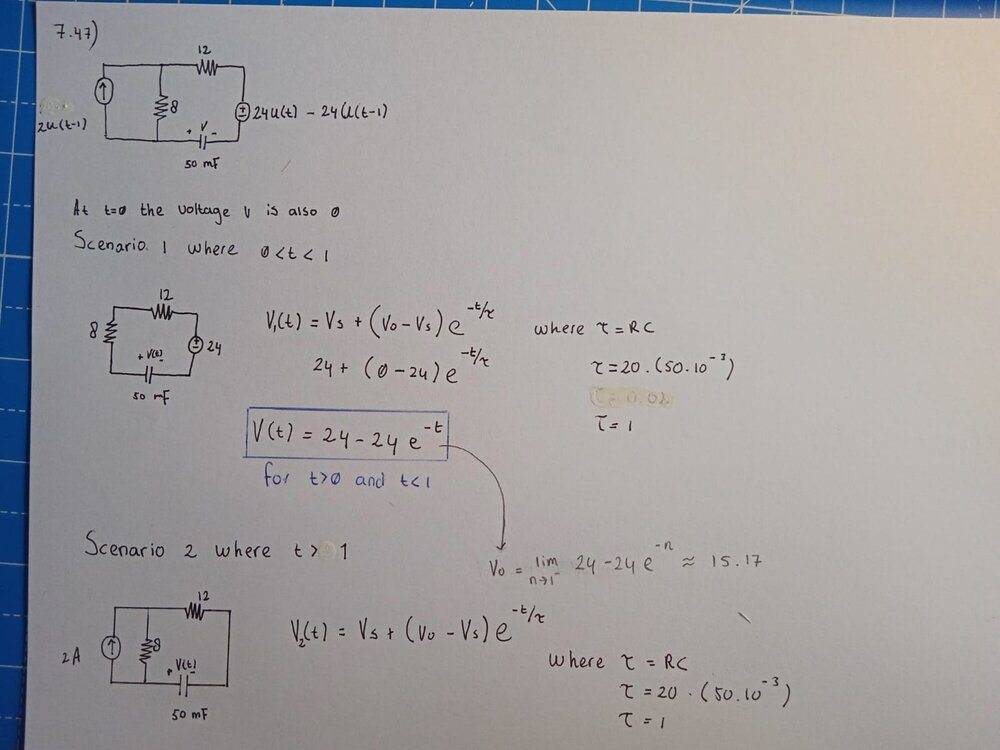
For the scenario 0 < t < 1 the current source is off and the voltage source Vs is 24V. Filling in the formula gives us 24-24e^(-t) which agrees on the answer sheet.
However, for scenario 2 we need to find Vo just before t = 1. I do that by using the previous formula and that gives me approximately 15.17V.
However, I am not quite sure how to find Vs in the second scenario between I am not quite sure what is happening in the circuit. The capacitor will first act as a short circuit but looks to DC as an open circuit so will current flow through the 8 and 12 ohm resistor or only the 8 ohm resistor?

However, I cannot seem to find the second part of the answer in the book for the time interval t > 1

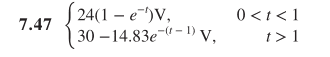
Could anyone clarify what is happening for t > 1?

 

[gneill]

For t > 1 you might find it convenient to first convert the current source and its parallel resistor to an equivalent voltage source and series resistance.

 

[Xhendos]

For t > 1 you might find it convenient to first convert the current source and its parallel resistor to an equivalent voltage source and series resistance.

Thanks for your tip. If I convert the circuit using source transformation principle I do get 16V voltage source in series with the 8 ohm resistor. However, according to the answer sheet we have to get Vs = 30V. Where does this delta of 14V from my answer compared to the correct answer sheet come from?

 

[gneill]

First recall that in this scenario the capacitor starts with an initial potential difference of 15.17 V. How did it get there?

The capacitor acts an an open circuit to DC only if it's potential difference matches any applied potential at that instant. In the first scenario the capacitor started out uncharged (zero potential difference) and the circuit's voltage source drove charge onto the capacitor. Thus current flowed.

For the second scenario it will help to convert the initially charged capacitor into an equivalent circuit model wherein you separate the capacitance and initial potential difference as separate components. This is an allowed operation for circuit analysis purposes. Just keep in mind that the "real" capacitor is now the combination of these two components. Something like this:

Here the "new" capacitor element begins uncharged, the previous charge that was on the original has been split off into the "new" voltage source. Continue your analysis from there.

 

[Xhendos]

First recall that in this scenario the capacitor starts with an initial potential difference of 15.17 V. How did it get there?

The capacitor acts an an open circuit to DC only if it's potential difference matches any applied potential at that instant. In the first scenario the capacitor started out uncharged (zero potential difference) and the circuit's voltage source drove charge onto the capacitor. Thus current flowed.

For the second scenario it will help to convert the initially charged capacitor into an equivalent circuit model wherein you separate the capacitance and initial potential difference as separate components. This is an allowed operation for circuit analysis purposes. Just keep in mind that the "real" capacitor is now the combination of these two components. Something like this:
View attachment 276496
Here the "new" capacitor element begins uncharged, the previous charge that was on the original has been split off into the "new" voltage source. Continue your analysis from there.

In this scenario I would add the two voltage sources to get Vo = 31.171V. Knowing that the 15.171V is stored energy and not an "ideal" voltage source just like the 16V voltage source means that the circuit would eventually decay to 16V over time, thus Vs = 16V

This would give V(t) = 31.171 + (31.171 - 16) e^(-t) which is equal to V(t) = 31.171 + 15.171e^(-t). However, the answer sheets states that Vs = 30V instead of our 31.171V. Where does this decrease of 1.171V comes from in Vs?

 

[gneill]

The 15.171V source of the equivalent circuit does not decay. It is a permanent ideal component of the equivalent circuit. When interpreting the potential difference across the "real" capacitor from the model version, you need to include this source.

What you can find from the equivalent circuit model is how the potential changes on its capacitor from it's initial uncharged state and forward in time. The "real" capacitor potential would be this potential summed with the model's voltage source.

What has happened is that they've tried to simplify the equation parameters a bit. Note that 30 - 14.83 = 15.17, which is the initial starting potential on the "real" capacitor.

However, I don't agree with their equation for the second scenario. When the circuit reaches steady state at large t, they would put the potential across the capacitor at 30 V, and I don't see any way for what is effectively a 16 V source to achieve that. I'm pretty sure that the end result for Vc (as defined in the schematic) at large time should be -16 V, not 30 V.

 

[Xhendos]

The 15.171V source of the equivalent circuit does not decay. It is a permanent ideal component of the equivalent circuit. When interpreting the potential difference across the "real" capacitor from the model version, you need to include this source.

This does not make sense to me. The capacitor is charged via an ideal voltage source. It temporarry stores the energy. Why would we threat the 15.171V source as an permanent ideal comoponent since it is not. The stored energy does decay. That is why a final voltage for a large t of -16V does make sense indeed.

 

[gneill]

This does not make sense to me. The capacitor is charged via an ideal voltage source. It temporarry stores the energy. Why would we threat the 15.171V source as an permanent ideal comoponent since it is not. The stored energy does decay. That is why a final voltage for a large t of -16V does make sense indeed.

Yes this modeled source is the result of a charging process, but it is not a temporary charged component in the equivalent circuit. The charging up took place prior to this equivalent model taking over the role of the capacitor, and as such that initial potential difference is represented by a fixed voltage source. Rather than this voltage source changing value over time, the potential change on the other component of the model, an initially uncharged capacitor, will compensate.

In this case the real capacitor goes from a charge of +15.17 V downto -16 V, a total change of 31.17 V. The capacitor in the equivalent model goes from zero to 31.17 V. To find the final voltage on the "real" capacitor you need to compensate for the voltage source in the equivalent circuit, in this case by subtracting it from the potential on the model capacitor.