Capacitor problem with a beam balance -- balancing after changing the charge

Please provide more context.In summary, the conversation discusses a parallel plate capacitor and its components, including a lower plate supported by a rigid rod, an upper plate suspended from a balance, and a thin wire connecting the two plates. After the plates are disconnected and the balance is counterpoised, a voltage of 5000V is applied between the plates. The distance between the plates is 5mm and the area of each plate is 100sq.cm. The question then asks for the additional mass needed to maintain balance, assuming all elements other than the plates are massless and non-conducting. The suggested equation is Q^2d/2A ×epsilonnot = mg, using the principle of virtual work.
  • #1
Victim
22
1
New poster has been reminded to show the Relevant Equations and their Attempt at the Solution in schoolwork posts
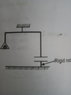
The lower plate of a parallel plate capacitor is supported on a rigid rod.The upper plate is suspended from one end of a balance.The two plates are joined together by a thin wire and subsequently disconnected.The balance is then counterpoised.Now a voltage V= 5000V is applied between the plates.The distance between the plates is d=5mm and the area of each plate is A=100sq.cm. Then find out additional mass placed to maintain balance.All the elements other than plates are massless and non conducting.

Homework Equations

The Attempt at a Solution

 

Attachments

  • 15339937343242138949623.jpg
    15339937343242138949623.jpg
    14.4 KB · Views: 470
Physics news on Phys.org
  • #2
I don't see an attempt at a solution. Hint - try using the principle of virtual work.
 
  • #3
phyzguy said:
I don't see an attempt at a solution. Hint - try using the principle of virtual work.
I had done Q^2d/2A ×apsilonnot =mg
 
  • #4
Where did that equation come from?
 

Related to Capacitor problem with a beam balance -- balancing after changing the charge

1. How does changing the charge on a capacitor affect the balance of a beam balance?

Changing the charge on a capacitor can alter its weight, which can impact the balance of a beam balance. Depending on the amount and direction of the charge, the beam balance may become unbalanced or shift to one side.

2. What factors can cause a capacitor to become imbalanced on a beam balance?

Aside from changing the charge, other factors that can affect the balance of a capacitor on a beam balance include its size, shape, and material composition. Additionally, external forces such as gravity, air currents, and vibrations can also play a role in disrupting the balance.

3. How can one accurately balance a capacitor on a beam balance after changing the charge?

To accurately balance a capacitor on a beam balance after changing the charge, it is important to ensure that the capacitor is placed at the exact center of the balance and that the balance is properly calibrated. Additionally, taking multiple readings and averaging them can help to minimize any discrepancies.

4. What are some potential solutions to a capacitor balance problem on a beam balance?

If a capacitor is consistently imbalanced on a beam balance, some potential solutions could include using a different type of capacitor with a more stable weight, adjusting the positioning of the capacitor on the balance, or using counterweights to balance out the weight of the capacitor.

5. Are there any safety precautions to consider when working with capacitors on a beam balance?

Yes, it is important to handle capacitors with caution as they can hold an electrical charge. Make sure to discharge the capacitor before removing it from the beam balance, and always wear protective gear such as gloves and goggles when handling electrical components.

Similar threads

Charge on a grounded conducting sphere in a uniform electric field, after ungrounding and movement
    • Introductory Physics Homework Help
Replies
1
Views
374
Uncharged capacitors connected in series
    • Introductory Physics Homework Help
Replies
18
Views
2K
I Thought I Understood Gauss' Law (Sheets)
    • Introductory Physics Homework Help
Replies
26
Views
893
How capacitance, charge, and energy stored changes on a capacitor?
    • Introductory Physics Homework Help
Replies
10
Views
3K
Find the capacitance of a half-full capacitor
    • Introductory Physics Homework Help
Replies
12
Views
2K
Changes in capacitor after dielectric inserted
    • Introductory Physics Homework Help
Replies
17
Views
2K
Does Separating the Plates of a Capacitor Affect Its Charge?
    • Introductory Physics Homework Help
Replies
13
Views
2K
Electric field in a capacitor with a dielectric
    • Introductory Physics Homework Help
Replies
5
Views
2K
Capacitance and induced charges
    • Introductory Physics Homework Help
Replies
14
Views
4K
Electrostatic energy after a metal piece is inserted between 2 capacitor plates
    • Introductory Physics Homework Help
Replies
12
Views
2K

Hot Threads

Recent Insights

Back
Top