joker_900
- 53
- 0
Capacitors - please, need urgent help!
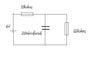
I've attached the circuit diagram but it's basically a cell connected in series with a 10kohm resistor, and then a 20microfarad capacitor and 22kohm resistor connected in parallel.
The capacitor begins charging at t=0. Show that the voltage across the capacitor as a function of time is Vc(t)=4.125(1 - exp(-t/0.1375))
Well i know that in a simple one resistor one capacitor series circuit, the current through the resistor is I=I0e^(-t/RC), and the voltage across the resistor is V=V0e^(-t/RC) (where V0=EMF)
Now i thought this same relationship might apply to the 10kohm (R1) resistor, as initially it's voltage = EMF, and as the capacitor charges, Vc increases and the voltage across R1 therefore decreases. However, in this situation, there is always current flow and so the voltage across R1 does not become zero.
I thought about applying kirchhoffs current law, but this did not seem to get me anywhere.
I am thoroughly confused, PLEASE HELP!
Thanks
Homework Statement
I've attached the circuit diagram but it's basically a cell connected in series with a 10kohm resistor, and then a 20microfarad capacitor and 22kohm resistor connected in parallel.
The capacitor begins charging at t=0. Show that the voltage across the capacitor as a function of time is Vc(t)=4.125(1 - exp(-t/0.1375))
Homework Equations
The Attempt at a Solution
Well i know that in a simple one resistor one capacitor series circuit, the current through the resistor is I=I0e^(-t/RC), and the voltage across the resistor is V=V0e^(-t/RC) (where V0=EMF)
Now i thought this same relationship might apply to the 10kohm (R1) resistor, as initially it's voltage = EMF, and as the capacitor charges, Vc increases and the voltage across R1 therefore decreases. However, in this situation, there is always current flow and so the voltage across R1 does not become zero.
I thought about applying kirchhoffs current law, but this did not seem to get me anywhere.
I am thoroughly confused, PLEASE HELP!
Thanks