- #1
jisbon
- 476
- 30
- Homework Statement
- Consider the circuit below. The switch is closed for a long time, then is opened. Calculate the time taken for ##15\mu F## capacitor to reach P.D of 2V.
- Relevant Equations
- ##Q(t) =Q_{0}e^{\frac {-t}{RC}}##
Firstly, I'm given this complicated circuit as shown below.

What I have to do first, is to simplify it, which I will need help in checking.
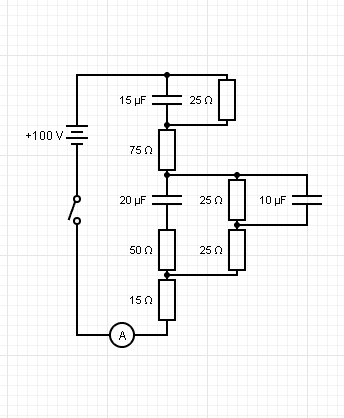
One question here: It's not possible to simplify this by adding resistors in series and capacitors in series am I, right? Or is it possible in this case?
So if I'm right, the next step to do find the charge in the ##15\mu## F capacitor after a long time, which is capacitance * voltage, which is presumably be 15V in this case? Hence ##Q_{0}## = ##15\mu## F * 100V ?
So for it to reach P.D of 2V, I will have to calculate the charge at that point. Since charge = capacitance * voltage, my charge at that point will be ##15\mu## * 2V = ##30*10^-6##
I will then use this formula where: ##Q(t) =Q_{0}e^{\frac {-t}{RC}}##
## 30*10^-6=(15*10^-6)(100)e^{\frac {-t}{RC}}##
Will R in this case be 25?
Thanks.
What I have to do first, is to simplify it, which I will need help in checking.
One question here: It's not possible to simplify this by adding resistors in series and capacitors in series am I, right? Or is it possible in this case?
So if I'm right, the next step to do find the charge in the ##15\mu## F capacitor after a long time, which is capacitance * voltage, which is presumably be 15V in this case? Hence ##Q_{0}## = ##15\mu## F * 100V ?
So for it to reach P.D of 2V, I will have to calculate the charge at that point. Since charge = capacitance * voltage, my charge at that point will be ##15\mu## * 2V = ##30*10^-6##
I will then use this formula where: ##Q(t) =Q_{0}e^{\frac {-t}{RC}}##
## 30*10^-6=(15*10^-6)(100)e^{\frac {-t}{RC}}##
Will R in this case be 25?
Thanks.