Joshua Pham
- 14
- 0
Hey guys,
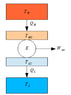
I ran into this paper talking about the Maximum power you can obtain from a Carnot cycle: http://aapt.scitation.org/doi/abs/10.1119/1.10023 From what I understood, there are two extremes. To achieve maximum efficiency you have to make sure that the temperature of the system is never more than infinitesmally out of thermal equilibrium with its thermal reservoirs. So during the isothermal expansion, you have heat transfer coming in albeit at a very slow rate because of the negligible temperature difference between the hot reservoir and the system. It then isentropically expands to its low temperature which is infinitesmally higher than the cold reservoir and you get heat transfer out.
The other extreme is when you set the system temperature so that it does not change during the isothermal processes. From the paper this leads to all of the heat going straight from the hot sink to the cold sink and 0 power output. I don't quite understand this bit. Why does all of the heat go straight from the hot to cold sink?
I ran into this paper talking about the Maximum power you can obtain from a Carnot cycle: http://aapt.scitation.org/doi/abs/10.1119/1.10023 From what I understood, there are two extremes. To achieve maximum efficiency you have to make sure that the temperature of the system is never more than infinitesmally out of thermal equilibrium with its thermal reservoirs. So during the isothermal expansion, you have heat transfer coming in albeit at a very slow rate because of the negligible temperature difference between the hot reservoir and the system. It then isentropically expands to its low temperature which is infinitesmally higher than the cold reservoir and you get heat transfer out.
The other extreme is when you set the system temperature so that it does not change during the isothermal processes. From the paper this leads to all of the heat going straight from the hot sink to the cold sink and 0 power output. I don't quite understand this bit. Why does all of the heat go straight from the hot to cold sink?