Cartesian coordinates vs. The rest of the world?

[ManDay]

So I wonder why the gradient in coordniates other than cartesian ones bears coefficients. Let's take spherical coordinates for example. We have

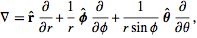
(Source) - Sorry if image doesn't work - too lazy to get the TeX right.[/size]

From what I know, I don't see anything that raises cartesian coordinates above any other C/S' (apart from marginal properties such as whether the mapping is reversable). I hence would expect the gradient in spherical coordinates to be

\vec\nabla = \vec{e}_r\frac{d}{dr} + \vec{e}_\phi\frac{d}{d\phi} + \vec{e}_\theta\frac{d}{d\theta},

where \vec{e}_\dots is the unit vector in \vec{g}_{\dots} = \frac{\partial \vec{r}}{\partial \dots} direction (where |g| is not normalized).

After all, the gradient in coordinate q descibes the change of intensity I in q direction. And when I change \vec{r} by a little d\theta, the change in intensity is naturally \frac{dI}{d\phi} and not \frac{1}{r\sin(\phi)}\frac{\partial I}{\partial \theta} (why would it be partial anyway?).

So why is transformed from cartesian coordinates? What validates cartesian coordinates as the origin of all transforms, so to say? I could understand the application of the Leibniz'en chain rule if \nabla to a scalar potential in general coordinates were sought with respects to cartesian coordinates. But we are looking for the gradient in terms of spherical coordinates - so what do cartesian coordinates want to tamper with?best regards

 

[HallsofIvy]

I'm not sure why you think the gradient having constant coefficients (or, equivalently, that the metric tensor is a constant function of the coordinates) "raises Cartesian coordinates above other coodinates". The crucial point is that Cartesian coordinates are based on straight lines. Because calculus itself is based on straight lines (the derivative is basically a way of approximating a function by a linear function), of course, such a coordinate system is simpler than others. It is largely an artifact of the way we have developed calculus. It would be possible to develop a calculus based on curvilinear coordinates, approximating a functions graph, not by a straight line but by some other curve. If we developed a calculus based on circles, then polar coordinates would give particularly simple gradients.

 

[zhentil]

How can you argue with a definition? You may think that the gradient should be defined a certain way, but it wasn't. You're free to define an s-gradient, however.

 

[ManDay]

HallsofIvy, much appreciated. But can you come up with a more graphical explanation for why there are these coefficients? Do they somewhat normalize the gradient with respect to the metric - because that's the impression I have? Yet, I wouldn't see a reason why it's useful.

 

[g_edgar]

If I travel due east at a speed of 1 km per hour for 1 hour, how much change is there in my longitude? (Assume my latitude and altitude remain constant.) In fact, the answer depends on my latitude! (And on my altitude...)