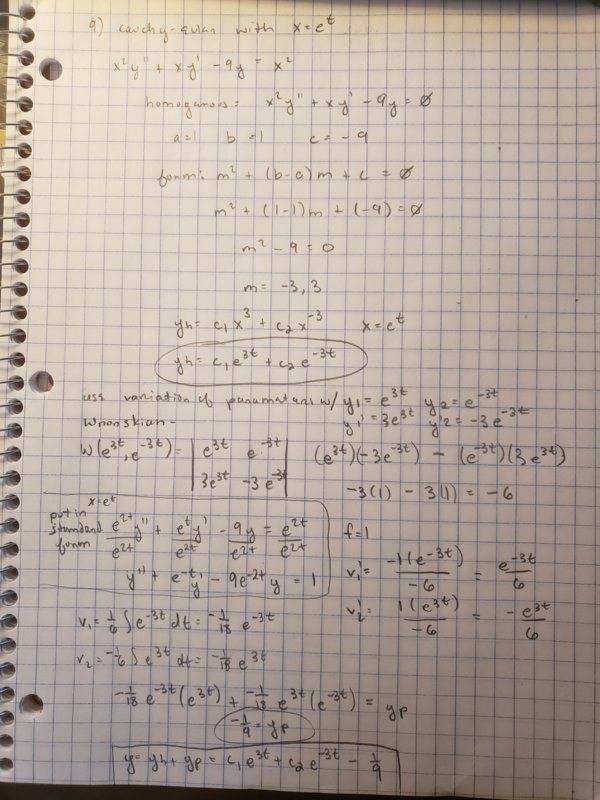kepherax
- 9
- 1
- Homework Statement
- Use Cauchy-Euler method with x=e^t to solve the following differential equation.
- Relevant Equations
- x^2y''(x)+xy'(x)-9y(x)=x^2
I'm fine with this up to a certain point, but I'm not certain if I'm using the substitution correctly. After finding the homogeneous solution do I plug in x= e^t in the original equation and then divide by e^2t to put it in standard form before applying variation of parameters so f=1, or do I just substitute so f= e^2t? The former is shown, but the latter gives a matching answer to plugging the original equation into symbolab if I were to replace their x with e^t. In videos I've watched and as per the book, you must always put the original equation into standard form and use the resulting f, but I feel like I'm missing something I can't put my finger on.