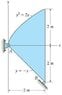
- #1
aaronfue
- 122
- 0
Homework Statement
I need to find the center of mass of the given figure attached. I am given the density (7850 kg/m^3) and a thickness of 0.3 cm (not sure where this goes)
Homework Equations
Just some things I need to verify:
When finding the x-bar of the function y=x3 using the equation:
[itex] \bar{x} [/itex]= [itex]\frac{∫ \tilde{x} dm}{∫dm}[/itex],
Is my [itex] \bar{x} [/itex] going to be the x distance(which will just be "x") times x3dm?
Also, will x3 be in the denominator just before "dm"?
If I am also given a density ρ, will that stay in front of each integrand or in front of ([itex]\frac{∫ \tilde{x} dm}{∫dm}[/itex])? And would I calculate the thickness with the [itex]\bar{z}[/itex]?
Is the same process is done for the [itex]\tilde{y}[/itex] or are there differences?
I know this may be a lot but I'd like to make sure of the method.
Thanks!
Homework Statement
Homework Equations
The Attempt at a Solution
Attachments
Last edited: