jonjacson
- 450
- 38
Hi to everybody
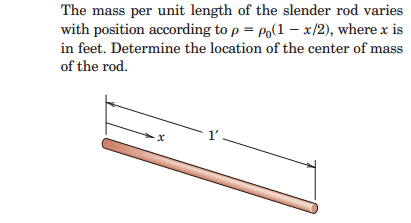
I´ll show the problem with a picture:
L\overline{x}=∫xc ρ dl
Well the total length of the rod is 1 feet, I only need to calculate the integral.
The moment xc of a differential element of mass of the rod is the distance x to the y axis, and the density is known so:
∫x * (1-x/2) dx , from 0 to 1, the result for me is:
1 * \overline{x} = 1/3
So \overline{x}= 1/3;
Unfortunately the result is 4/9, I can´t see where are my mistakes, maybe I´m not using the proper arm length or something.
The problem doesn´t give you any coordinate system, only the x axis, I assume that the y-axis is orthogonal, and the equation for the moments around that axis gives you the x center of mass.
I suppose that nothing would change if I had used another coordinate system, Am I right?
I assumed too that the constant ρ0 at the equation for the density would not change anything, but maybe that is a mistake.
Where are my mistakes?
Homework Statement
I´ll show the problem with a picture:
Homework Equations
L\overline{x}=∫xc ρ dl
The Attempt at a Solution
Well the total length of the rod is 1 feet, I only need to calculate the integral.
The moment xc of a differential element of mass of the rod is the distance x to the y axis, and the density is known so:
∫x * (1-x/2) dx , from 0 to 1, the result for me is:
1 * \overline{x} = 1/3
So \overline{x}= 1/3;
Unfortunately the result is 4/9, I can´t see where are my mistakes, maybe I´m not using the proper arm length or something.
The problem doesn´t give you any coordinate system, only the x axis, I assume that the y-axis is orthogonal, and the equation for the moments around that axis gives you the x center of mass.
I suppose that nothing would change if I had used another coordinate system, Am I right?
I assumed too that the constant ρ0 at the equation for the density would not change anything, but maybe that is a mistake.
Where are my mistakes?