DaviBones
- 7
- 0
Homework Statement
In the 1968 Olympic Games, University of Oregon jumper Dick Fosbury introduced a new technique of high jumping called the "Fosbury flop." It contributed to raising the world record by about 30 cm and is presently used by nearly every world-class jumper. In this technique, the jumper goes over the bar face up while arching his back as much as possible, as shown below. This action places his center of mass outside his body, below his back. As his body goes over the bar, his center of mass passes below the bar. Because a given energy input implies a certain elevation for his center of mass, the action of arching his back means his body is higher than if his back were straight. As a model, consider the jumper as a thin, uniform rod of length L. When the rod is straight, its center of mass is at its center. Now bend the rod in a circular arc so that it subtends an angle of θ = 80.5° at the center of the arc, as shown in Figure (b) below. In this configuration, how far outside the rod is the center of mass? Report your answer as a multiple of the rod length L.
http://www.webassign.net/pse/p9-44alt.gif
Homework Equations
L=rθ
where L is arc (rod) length.
r_{cm}=\int r \: dm
The Attempt at a Solution
So the TA for my discussion section said it was far too advanced to expect us to do it on our own, and did a healthy amount of work for us by giving us this equation...
y_{cm}=\frac{1}{M}\int ^{ \theta / 2 }_{ - \theta / 2 } r cos\left(\theta \right) \frac{M}{L} r \: d\theta
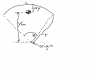
I've attached a picture showing what the different variables I use are. Sadly, since I think this might be where my problem is, I don't remember how he derived this, but I know it was using the equations in the "relevant equations" section, and possibly using linear momentum as well, although I'm not sure.
So I took his equation, pulled out r, L, and M, and integrated.
y_{cm}=\frac{r^{2}}{L} \left( sin\left(\frac{\theta}{2} \right) - sin\left(\frac{-\theta}{2} \right) \right)
Plugging in (L/θ) for r gives...
y_{cm}=\frac{L}{\theta^{2}} \left( sin\left(\frac{\theta}{2} \right) - sin\left(\frac{-\theta}{2} \right) \right)
Lastly, (since I'm looking for Δy, not y_cm) I used
Δy = r - y_cm
and
r=(L/θ)
to give me
\Delta y=\frac{L}{θ} - \frac{L}{\theta^{2}} \left( sin\left(\frac{\theta}{2} \right) - sin\left(\frac{-\theta}{2} \right) \right)
By factoring out L and computing with θ=(80.5π/180) i get .699L ... Which isn't right, which is why I'm here. I'm not sure if the equation given to me by my TA was wrong, or if I didn't integrate right, or what, but I'm stumped..
Thanks in advance for any help.