dchartier
- 13
- 1
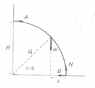
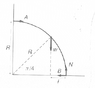
On page 252 of Kleppner's Introduction to Mechanics (2d. Ed.) in Example 7.5, Kleppner analyzes the forces and torques on a uniform rod that have been bent into a quarter-circle of radius R and length PI*R/2. His diagram is attached.
Kleppner writes, "[t]he center of mass is halfway along the rod at PI*R/2.'' In the diagram, you see this is the point on the rod at its midway point (at polar coordinates (R, PI/4), where the weight vector W is shown).
I'm not sure how he places the center of mass at this point. I calculated the center of mass as at polar coordinates (2^(3/2) R/PI, PI/4). I calculated it as follows. The mass per unit length is:
\begin{equation*}
\lambda = \frac{M}{\frac{2 \pi R}{4}} = \frac{2M}{\pi R}
\end{equation*}
I calculated the center of mass as:
\begin{equation*}
\frac{1}{M} \int_C \boldsymbol{r} dm = \frac{1}{M} \int_0^{\pi/2} R (\boldsymbol{a_x} \cos \theta + \boldsymbol{a_y} \sin \theta ) \lambda R d\theta =
\end{equation*}
\begin{equation*}
\frac{2R}{\pi} \int_0^{\pi/2} (\boldsymbol{a_x} \cos \theta + \boldsymbol{a_y} \sin \theta) d\theta =
\left. \frac{2R}{\pi} (\boldsymbol{a_x} \sin \theta - \boldsymbol{a_y} \cos \theta ) \right|_0^{\pi /2} =
\end{equation*}
\begin{equation*}
\frac{2R}{\pi} (\boldsymbol{a_x} + \boldsymbol{a_y}) = \boldsymbol{a_r} \frac{2 \sqrt{2} R}{\pi} + \boldsymbol{a_\theta} \frac{\pi}{4}
\end{equation*}
This places the center of mass at (2^(3/2) R/PI, PI/4), or about 90% of the distance from the origin to the rod. Kleppner seems to say the center of mass is on the rod itself. Did I make a mistake?
Many thanks for your help!
Kleppner writes, "[t]he center of mass is halfway along the rod at PI*R/2.'' In the diagram, you see this is the point on the rod at its midway point (at polar coordinates (R, PI/4), where the weight vector W is shown).
I'm not sure how he places the center of mass at this point. I calculated the center of mass as at polar coordinates (2^(3/2) R/PI, PI/4). I calculated it as follows. The mass per unit length is:
\begin{equation*}
\lambda = \frac{M}{\frac{2 \pi R}{4}} = \frac{2M}{\pi R}
\end{equation*}
I calculated the center of mass as:
\begin{equation*}
\frac{1}{M} \int_C \boldsymbol{r} dm = \frac{1}{M} \int_0^{\pi/2} R (\boldsymbol{a_x} \cos \theta + \boldsymbol{a_y} \sin \theta ) \lambda R d\theta =
\end{equation*}
\begin{equation*}
\frac{2R}{\pi} \int_0^{\pi/2} (\boldsymbol{a_x} \cos \theta + \boldsymbol{a_y} \sin \theta) d\theta =
\left. \frac{2R}{\pi} (\boldsymbol{a_x} \sin \theta - \boldsymbol{a_y} \cos \theta ) \right|_0^{\pi /2} =
\end{equation*}
\begin{equation*}
\frac{2R}{\pi} (\boldsymbol{a_x} + \boldsymbol{a_y}) = \boldsymbol{a_r} \frac{2 \sqrt{2} R}{\pi} + \boldsymbol{a_\theta} \frac{\pi}{4}
\end{equation*}
This places the center of mass at (2^(3/2) R/PI, PI/4), or about 90% of the distance from the origin to the rod. Kleppner seems to say the center of mass is on the rod itself. Did I make a mistake?
Many thanks for your help!
Attachments
Last edited: