Centripetal force basic questions

[sameeralord]

Hello guys,

I wasn't interested in these stuff those days and I never got it.

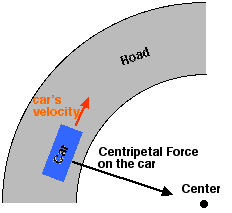
Now when you do a car turn the friction from the tires provide the centripetal force right. I have few quick questions. How does the friction from tires give a force in the centripetal direction, how come it is not in the direction that is opposite to velocity direction? If the centripetal force is towards the centre why is car going in a circle, wouldn't it be sucked into the centre, Am I missing some resulting forces? Thanks guys

 

[rcgldr]

The tires exert an outwards force onto the pavement, which responds with an equal and opposing inwards force onto the tires (the Newton 3rd law pair of forces). This inwards centripetal force on the tires is then transmitted to the axles, suspension, body, and the occupants of the car.

At the same time the outwards force from the tires casues the the Earth to be moved a tiny amount "outwards", but since it's so massive, it's generally considered not to be moved at all.

The reason the tires genreate a force perpendicular to the direction of travel is that they're oriented slightly inwards of the actual direction the car is moving, including the rear tires (the entire car is yawed slightly inwards in a corner). This results in a deformation at the contact patch that produces the outward force on the pavement. The pavement also deforms, but by a very small amount and this coresponds to the inwards force from the pavement to the tires at the contact patch.

The car only goes in a circle if the centripetal force exactly equals speed²/r. Otherwise the path is a spiral.

 

[sameeralord]

The tires exert an outwards force onto the pavement, which responds with an equal and opposing inwards force onto the tires (the Newton 3rd law pair of forces). This inwards centripetal force on the tires is then transmitted to the axles, suspension, body, and the occupants of the car.

At the same time the outwards force from the tires casues the the Earth to be moved a tiny amount "outwards", but since it's so massive, it's generally considered not to be moved at all.

The reason the tires genreate a force perpendicular to the direction of travel is that they're oriented slightly inwards of the actual direction the car is moving, including the rear tires (the entire car is yawed slightly inwards in a corner). This results in a deformation at the contact patch that produces the outward force on the pavement. The pavement also deforms, but by a very small amount and this coresponds to the inwards force from the pavement to the tires at the contact patch.

Thanks again Jeff However I'm still confused why the car is not sucked in by the centripetal force why is velocity and car moving in another direction. Isn't the force towards the centre?

 

[rcgldr]

However I'm still confused why the car is not sucked in by the centripetal force why is velocity and car moving in another direction. Isn't the force towards the centre?

I posted before I was done editting my response, the path is only a circle when the centripetal force = speed² / radius. Otherwise it's a spiral, inwards if the force is greater, outwards if the force is less.

 

[sameeralord]

I posted before I was done editting my response, the path is only a circle when the centripetal force = speed² / radius. Otherwise it's a spiral, inwards if the force is greater, outwards if the force is less.

Thanks but if I consider this force like gravity it would suck the car, I mean isn't the directiion of velocity dependent on the direction of force. Is their some component vector I'm missing. I mean how is the car overcoming inward force.

 

[sganesh88]

Force and velocity don't have the same direction. Consider a ball thrown upward. The velocity is up, force from gravity(and acceleration) is down.

 

[sameeralord]

Oh I was just rusty with physics. I see the car wants to travel in a straight line and it is centripetal force that makes it go in a circle. Thanks Jeff and sganesh for the help