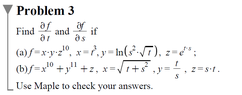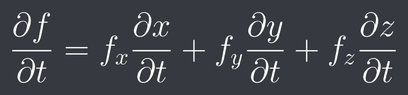Using Chain Rule to Solve Questions - A Step-by-Step Guide
- Context: MHB
- Thread starter EconometricAli
- Start date
-
- Tags
- Chain Chain rule
Click For Summary
This discussion focuses on applying the chain rule in multivariable calculus to solve specific problems involving functions of multiple variables. The chain rule is defined as $\frac{\partial f}{\partial t}= f_x\frac{\partial x}{\partial t}+ f_y\frac{\partial y}{\partial t}+ f_z\frac{\partial z}{\partial t}$ and $\frac{\partial f}{\partial s}= f_x\frac{\partial x}{\partial s}+ f_y\frac{\partial y}{\partial s}+ f_z\frac{\partial z}{\partial s}$. Participants worked through examples such as $f(x, y, z)= xyz^{10}$ and $f= x^{10}+ y^{11}+ z$, detailing the necessary partial derivatives and substitutions. The discussion highlights common pitfalls in applying the chain rule and emphasizes the importance of correctly identifying each variable's dependency.
PREREQUISITES- Understanding of multivariable calculus concepts
- Familiarity with partial derivatives
- Knowledge of the chain rule in calculus
- Basic algebraic manipulation skills
- Practice solving multivariable calculus problems using the chain rule
- Study the derivation and applications of the chain rule in different contexts
- Learn about implicit differentiation and its relationship to the chain rule
- Explore advanced topics in multivariable calculus, such as Jacobians and Hessians
Students and professionals in mathematics, engineering, and physics who need to apply the chain rule in multivariable calculus problems. This discussion is particularly beneficial for those preparing for exams or working on complex calculus assignments.
Similar threads
- · Replies 5 ·
- · Replies 3 ·
- · Replies 1 ·
- · Replies 1 ·
- · Replies 7 ·
- · Replies 4 ·
- · Replies 10 ·
- · Replies 4 ·
- · Replies 1 ·
- · Replies 20 ·