Change in Capacitor for largest possible Current

In summary, the problem involves calculating the capacitive and inductive reactance, as well as the impedance, in a series RLC circuit with an alternating voltage source, a resistor, an inductor, and a capacitor. The goal is to determine the value of the capacitive reactance when the largest possible current is supplied by the source. The frequency of the source is 49.1 Hz and the inductor has an inductance of 55.9 mH. The capacitor has a capacitance of 2.55 mF and the resistor has a resistance of 21.1 Ω. The values for inductive reactance and capacitive reactance are 17.2 Ω and 1.27
  • #1
Jess_18033152
32
0

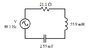
Homework Statement


The capacitor is changed so that the largest possible current is supplied by the source.
Enter the value of the capacitive reactance when this change is made.
Give your answer in Ohms (Ω). A unit is not required with your answer.

Homework Equations


The circuit is powered by an alternating voltage source, which produces a voltage that varies sinusoidally and has an RMS voltage of V.

- The frequency of the voltage source is 49.1 Hz and the inductor has an inductance of 55.9 mH.
Calculate the inductive reactance (XL) of the inductor.
Give your answer in units of Ohms (Ω) = 17.2

- The capacitor has a capacitance of 2.55 mF.
Calculate the capacitive reactance (XC) of the capacitor. The frequency is still 49.1 Hz.
Again, give your answer in units of Ohms (Ω) = 1.27

- The resistor has a resistance of 21.1 Ω.
Calculate the impedance (Z) of the RLC network.
Give your answer in units of Ohms (Ω) = 26.4

Im not sure what this question is asking me or what equation to use to calculate it either.
 
Physics news on Phys.org
  • #2
What is the sign of the capacitive reactance and inductive reactance?
 
  • #3
How are your components interconnected? Is it a series RLC circuit like this?

upload_2018-5-26_12-13-11.png
 

Attachments

  • upload_2018-5-26_12-13-11.png
    upload_2018-5-26_12-13-11.png
    1.5 KB · Views: 411

FAQ: Change in Capacitor for largest possible Current

How does changing the capacitance affect the maximum current in a circuit?

Increasing the capacitance in a circuit will decrease the maximum current, while decreasing the capacitance will increase the maximum current. This is because capacitance and current have an inverse relationship, meaning that as one increases, the other decreases.

What is the formula for calculating the maximum current in a circuit with a specific capacitance?

The formula for calculating maximum current in a circuit is I = C * ΔV/Δt, where I is the current in amperes, C is the capacitance in farads, ΔV is the change in voltage, and Δt is the change in time.

How does the type of capacitor affect the maximum current in a circuit?

The type of capacitor used in a circuit can affect the maximum current by changing the capacitance value. Different types of capacitors have different capacitance values, which means they will have different effects on the maximum current. For example, a ceramic capacitor will have a higher capacitance than an electrolytic capacitor of the same physical size.

Can changing the capacitance affect the stability of a circuit?

Yes, changing the capacitance in a circuit can affect the stability of the circuit. Capacitors are used to store charge and can help stabilize a circuit by smoothing out fluctuations in voltage. Changing the capacitance can disrupt this stabilization and potentially affect the performance of the circuit.

Is there a maximum capacitance limit for a circuit to maintain a stable maximum current?

Yes, there is a maximum capacitance limit for a circuit to maintain a stable maximum current. This limit depends on the other components in the circuit and their values. If the capacitance is too high, it can cause instability and potentially damage the circuit. It is important to carefully choose the appropriate capacitance for a circuit to ensure stability and proper functioning.

Similar threads

The phase difference between current and voltage.
Replies
30
Views
4K
The voltage across an AC source and a resistance in series
Replies
4
Views
1K
Calculation of current in driven series RLC circuit
Replies
8
Views
840
The relationship of the current before and after a change.
Replies
16
Views
2K
Changing capacitance effect on ripple in full rectification circuit
Replies
4
Views
2K
AC voltage across a parallel branch
Replies
5
Views
2K
What is the Resistance of the Patient in a Defibrillation Shock?
Replies
2
Views
1K
Find resistance of inductor in series RLC circuit
Replies
5
Views
2K
Calculating the Charge on Capacitor
Replies
8
Views
6K
But is it the same for AC circuits?
Replies
9
Views
1K

Hot Threads

Recent Insights

Back
Top