Change in potential energy of expanded air in piston-cylinder

[Danny_aero]

Air is heated in a vertical piston–cylinder assembly fitted with an electrical resistor. The volume of the air slowly increases by 1.6 ft^3 while its pressure remains constant. The area of the piston is 1 ft^2. The mass of the air is 0.6 lb. The local acceleration of gravity is g = 32.0 ft/s^2.

Question: Find the change in potential energy of the air in Btu.

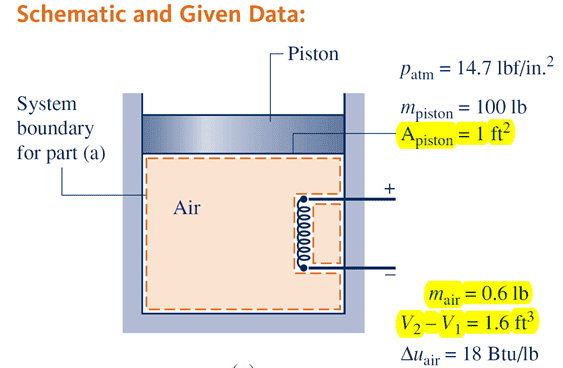
My calculation:

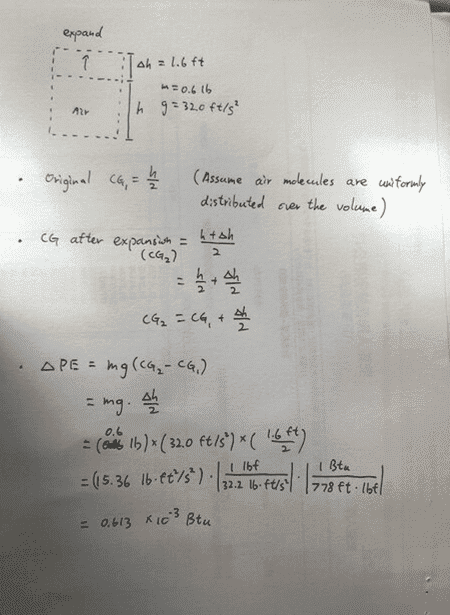
My answer is exact half as the book's answer.
I use the change of CG location to compute the elevation change. But it seems that the book uses the change of volume's top surface, which makes me confused. Shouldn't I use the height change of the CG instead of the height change of the top surface?

My thought is that:
If 1.6ft is used in height change, doesn't it mean that the whole volume and all the air molecules have risen for 1.6ft? But it shouldn't be the case, right? If the air is distributed evenly, there should be some air molecules stay on the bottom and some molecules move upwards for a little distance but absolutely not that much as 1.6ft higher. So, not all air molecules rise 1.6ft and ∆PE shouldn't be mg x (1.6ft).

 

[Lnewqban]

I agree with you.
If we would double the volume, the location of the new CG would at the height the bottom of the piston initially occupies.

 

[Chestermiller]

This problem from Moran et al clearly indicates that the change in potential energy of the air is negligible. In part b, they determine the change in internal energy of the piston (not the air) when they consider the piston as part of the "system." The vertical displacement of the piston times the weight of the piston is its change in potential energy.