jinksys
- 122
- 0
! SOLVED !
This isn't a homework problem, just an equation in my chapter. I don't see how the two integrals pointed to by the blue arrows become the integral pointed to by the red arrow. I know that if you swap the limits of integration, you change the sign of the integral. However, how do you change the -pi to pi in the second integral?
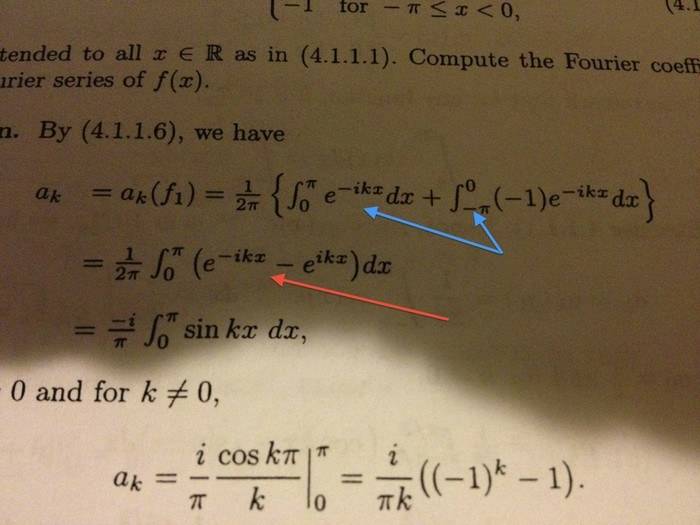
This isn't a homework problem, just an equation in my chapter. I don't see how the two integrals pointed to by the blue arrows become the integral pointed to by the red arrow. I know that if you swap the limits of integration, you change the sign of the integral. However, how do you change the -pi to pi in the second integral?
Last edited: